Scalar Triple Product of Vectors

There are two types of triple product of vectors

(a) Scalar Triple Product : $(\underline u\times\underline v).\underline w$ or $\underline u.(\underline v \times \underline w)$

(b) Vector Triple Product : $(\underline u\times\underline v)\times\underline w$

In this section, we shall study the scalar triple product only

Definition : let $\overrightarrow u$ = $a_1\underline i$ + $b_1\underline j$ + $c_1 \underline k$ , $\overrightarrow v$ = $a_2\underline i$ + $b_2\underline j$ + $c_2 \underline k$ , $\overrightarrow w$ = $a_3\underline i$ + $b_3\underline j$ + $c_3 \underline k$ The scalar triple product of vector $\overrightarrow u$ , $\overrightarrow v$ and $\overrightarrow w$ is defined by $\overrightarrow u$ . ( $\overrightarrow v$ × $\overrightarrow w$ ) or $\overrightarrow v$ .( $\overrightarrow w$ × $\overrightarrow u$ ) or $\overrightarrow w$ .( $\overrightarrow u$ × $\overrightarrow v$ ) The scalar triple product $\overrightarrow u$ . ( $\overrightarrow v$ × $\overrightarrow w$ $\overrightarrow w$ ) is written as $\overrightarrow u$ . ( $\overrightarrow v$ × $\overrightarrow w$ ) =[ $\underline u\;\underline v\;\underline w$ ]

Analytical Expression Of $\overrightarrow u$ . ( $\overrightarrow v$ $\overrightarrow w$ )

Let $\overrightarrow u$ = $a_1\underline i$ + $b_1\underline j$ + $c_1 \underline k$ , $\overrightarrow v$ = $a_2\underline i$ + $b_2\underline j$ + $c_2 \underline k$ , $\overrightarrow w$ = $a_3\underline i$ + $b_3\underline j$ + $c_3 \underline k$

Important Note : (1) The value of the triple scalar product depends upon the cycle order of the vectors , but is independent of the dot and cross. So the dot and cross , may be interchanged without alternating the value i.e; (2) ( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ = $\overrightarrow u$ ( $\overrightarrow v$ × $\overrightarrow w$ ) = [ $\underline u\;\underline v\;\underline w$ ]

( $\overrightarrow v$ × $\overrightarrow w$ ) $\overrightarrow u$ = $\overrightarrow v$ ( $\overrightarrow w$ × $\overrightarrow u$ ) = [ $\underline v\;\underline w\;\underline u$ ]

( $\overrightarrow w$ × $\overrightarrow u$ ) $\overrightarrow v$ = $\overrightarrow w$ ( $\overrightarrow u$ × $\overrightarrow v$ ) = [ $\underline w\;\underline u\;\underline v$ ]

(3) The value of the product changes if the order is non cyclic .

(4) ( $\overrightarrow u$ . $\overrightarrow v$ . $\overrightarrow w$ and $\overrightarrow u$ × ( $\overrightarrow v$ . $\overrightarrow w$ )

Applications Of Scalar Triple Product :

The Volume Of The Parallelepiped
The Volume Of The Tetrahedron

(1) The Volume Of The Parallelepiped :

The triple scalar product ( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ represents the volume of the parallelepiped having $\overrightarrow u$ , $\overrightarrow v$ and $\overrightarrow w$ as its conterminous edges. As it is seen from the formula that:

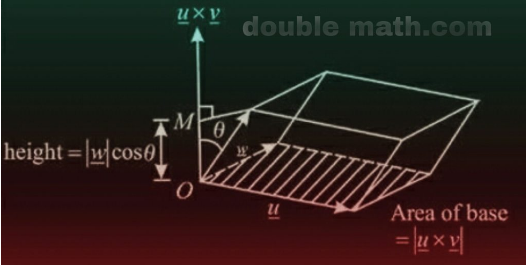
( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ = $\left| \overrightarrow u × \overrightarrow v \right|$ $\left| \overrightarrow w \right| \cos\theta$ Hence

(i) $\left| \overrightarrow u × \overrightarrow v \right|$ = area of the parallelogram with two adjacent sides, $\overrightarrow u$ and $\overrightarrow v$

(ii) $\left| \overrightarrow w \right| \cos\theta$ = height of the parallelepiped

( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ = $\left| \overrightarrow u × \overrightarrow v \right|$ $\left| \overrightarrow w \right| \cos\theta$ =(Area of parallelogram)(height)

= Volume of the parallelepiped Similarly, by taking the base plane formed by $\overrightarrow v$ and $\overrightarrow w$ , we have

The volume of the parallelepiped = ( $\overrightarrow v$ × $\overrightarrow w$ ) $\overrightarrow u$

And by taking the base plane formed by $] \overrightarrow w$ and $] \overrightarrow u$ , we have

The volume of the parallelepiped = ( $\overrightarrow w$ × $\overrightarrow u$ ) $\overrightarrow v$

So, we have: ( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ = ( $\overrightarrow v$ × $\overrightarrow w$ ) $\overrightarrow u$ = ( $\overrightarrow w$ × $\overrightarrow u$ ) $\overrightarrow v$

(2) The Volume Of The Tetrahedron :

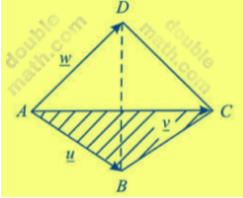
Volume of the tetrahedron ABCD
= $\frac13$ ( $\triangle$ ABC)(height of D above the place ABCD)

= $\frac13 \frac12 \left| \overrightarrow u × \overrightarrow v \right| (h)$

= $\frac16$ (Area of parallelogram with AB and AC as adjacent\)
= $\frac16$ (volume of the parallelogram with $\overrightarrow u$ , $\overrightarrow v$ , $\overrightarrow w$ as edges)

Thus volume = $\frac16 \overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ =[ [ $\frac16 \underline u\;\underline v\;\underline w$ ]

Properties of Triple scalar Product :

(1) If $\overrightarrow u$ , $\overrightarrow v$ and $\overrightarrow w$ are coplanar , then the volume of the parallelepiped so formed is zero i.e; the vectors $\overrightarrow u$ , $\overrightarrow v$ , $\overrightarrow w$ are coplanar $\Leftrightarrow$ ( $\overrightarrow u$ × $\overrightarrow v$ ) $\overrightarrow w$ =0

(2) If any two vectors of triple product are equal , then its value is zero i.e;

[ $\underline u\;\underline u\;\underline w$ ] = [ [ $\underline u\;\underline v\;\underline v$ ]

Analytical Expression Of . ( )

Applications Of Scalar Triple Product :

Leave a Comment Cancel Reply

Analytical Expression Of $\overrightarrow u$ . ( $\overrightarrow v$ $\overrightarrow w$ )