What is a 9 Sided Shape?
With nine straight sides that meet at nine corners make a polygon that is called a Nonagon. Nonagon is a 2D nine-sided shape that belongs to the family. The word “nonagon ” comes from the Latin word “nona “, meaning nine, and “gon “, meaning sides. So it literally means “9 sided shape “.
There are 9 straight sides and 9 vertices connecting these straight sides in a nonagon. The Sum of all the interior angles of a nine-sided polygon is equal to 1260 degrees.
In Greek, a nonagon is called an enneagon, which means “nine corners”.
Types of (Nonagon) 9 Sided Shape
There are two types of nonagon.
- Regular Nonagon
- Irregular Nonagon
Regular Nonagon
- It is a two-dimensional shape.
- It has nine vertices.
- Each interior angle is at 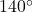140^\circ and the sum of these interior angles is 1260^\circ.
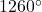- It’s all straight lines that have equal lengths.
- It has an exterior angle equal to 360 degrees.
- The regular nonagon has a symmetrical appearance and is considered a highly geometrically structured shape. It’s often used to demonstrate principles of symmetry and equality in geometry.
Irregular Nonagon
- The sum of all of its interior angles is 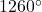1260^\circ degrees.
- Angles at varying degrees.
- It is a nine-sided, two-dimensional shape
- Additionally, it has straight lines
- The sides are not equal in length.
- Irregular nonagon does not have the symmetrical properties of a regular nonagon and can take on various shapes, making it more versatile in appearance.
9 sided Shapes in daily life and their role.
Nine sided Shape or nonagon used in various fields for example Stop sign is used to control traffic
Football: Some footballs are in nonagon shape that players use for better playing.
Garden: A nonagon shape might be considered for a better view in gardening.
Area of Nine-sided Shape (Nonagon) Examples
Question #1: Find the area of a regular nonagon with a side length of 8 units.
The formula for the area of regular Nonagon is
Area=\frac94\;l^2\;cot\left(\frac{\mathrm\pi}9\right)here l is the length of each side of nonagon(regular)
so,
Area=\frac94\;8^2\;cot\left(\frac{\mathrm\pi}9\right)</p> <p>[latex] Area=\frac94\;\left(64\;\right)\left(3.0777\right)Area= 554.784 square units