What is hyperbola:We have already stated that a conic section is a hyperbola if ![]() you can check. Let
you can check. Let ![]() and
and ![]() be a fixed point and
be a fixed point and ![]() be a line not containing
be a line not containing ![]() . Also let
. Also let ![]() be a point in the plane and
be a point in the plane and ![]() be the perpendicular distance of
be the perpendicular distance of ![]() from
from ![]() .
.
The set of all points ![]() such that
such that
![]()
is called a hyperbola.![]() and
and ![]() are respectively focus and directrix of the hyperbola
are respectively focus and directrix of the hyperbola ![]() is the eccentricity.
is the eccentricity.
Standard Equation of Hyperbola
Let ![]() be the focus with
be the focus with ![]() and
and ![]() be the directrix of the hyperbola.
be the directrix of the hyperbola.
Also, let ![]() be a point on the hyperbola, then by definition
be a point on the hyperbola, then by definition
![]() .
.
![]() .
.
![]() .
.
![]() .
.
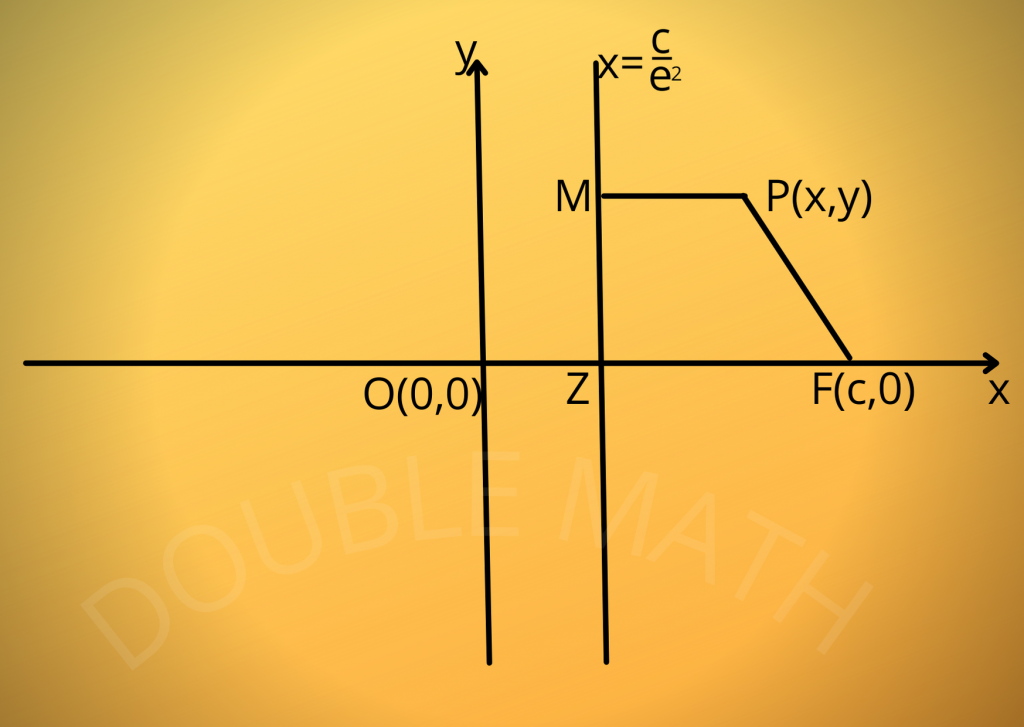
or
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
let us set ![]() , so that
, so that ![]() become
become
![]() .
.
![]() .
.
![]() .
.
![]() .
.
 .
.
where ![]() .
.
![]() is standard equation of Hyperbola
is standard equation of Hyperbola
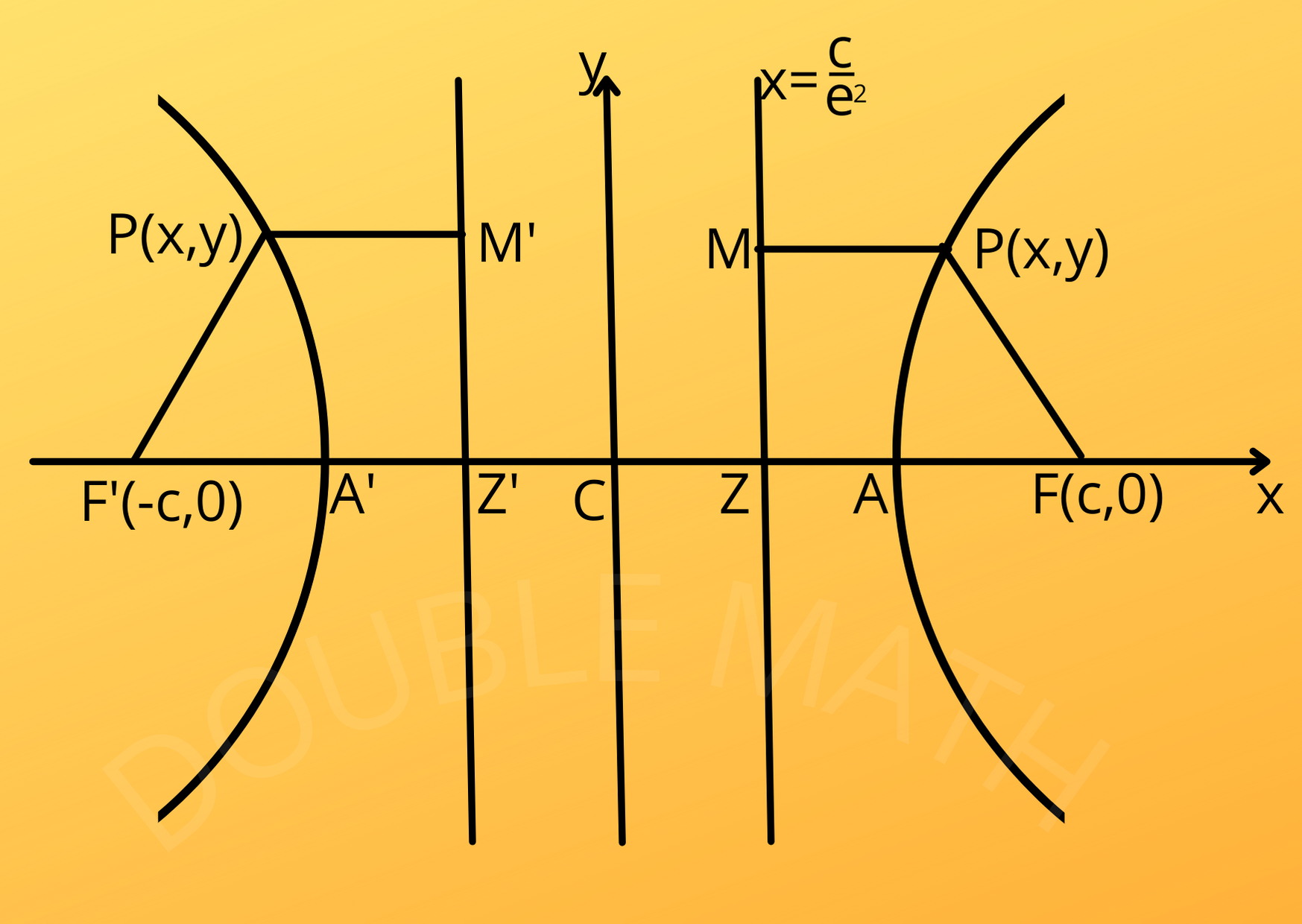
It is clear that the curve is symmetric with respect to both axes. If we take the point ![]() as focus and the line
as focus and the line ![]() as directrix, then it is easy to see that the set of all points
as directrix, then it is easy to see that the set of all points ![]() such that
such that
![]()
is a hyperbola with ![]() as its equation.
as its equation.
Thus a hyperbola has two foci and two directrices.
If the foci lie on the ![]() , then roles of
, then roles of ![]() and
and ![]() are interchanged in (3) and the equation
are interchanged in (3) and the equation
of the hyperbola becomes
![]() .
.
Definition: The hyperbola ![]() .
.
meets the x-axis at points with ![]() and
and ![]() . The points
. The points ![]() and
and ![]() are called vertices of the hyperbola. The line segment
are called vertices of the hyperbola. The line segment ![]() is called the transverse (or focal) axis of the hyperbola
is called the transverse (or focal) axis of the hyperbola ![]() . The equation
. The equation ![]() does not meet the y-axis in real points. However the line segment joining the points B(0, -b) and B’(0, b) is called the conjugate axis of the hyperbola. The midpoint
does not meet the y-axis in real points. However the line segment joining the points B(0, -b) and B’(0, b) is called the conjugate axis of the hyperbola. The midpoint ![]() of
of ![]() is called the centre of the hyperbola.
is called the centre of the hyperbola.
In the case of hyperbole (3), we have
![]() . The eccentricity
. The eccentricity ![]()
so that, unlike the ellipse, we may have ![]() or
or ![]() or
or ![]()
The point ![]() lies on the hyperbola
lies on the hyperbola ![]() for all real values of
for all real values of ![]() . The equations
. The equations ![]() are called parametric equations of the hyperbola.
are called parametric equations of the hyperbola.
Since
![]() when
when ![]()
![]()
The lines (2) do not meet the curve but the distance of any point on the curve from any of the two lines approaches zero. Such lines are called asymptotes of a curve. The joint equation of the asymptotes of (3) is obtained by writing 0 instead of 1 on the right-hand side of the standard form (3). Asymptotes are very helpful in graphing a hyperbola. The ellipse and hyperbola are called central conics because each has a center of symmetry.
