Erfi Imaginary Error Function

Introduction

Let x be a complex variable of C\backslash\;{\infty} .The function Imaginary Error Function
erfi is defined by the following second-order differential equation

-2x\;\frac{\partial y(x)}{\partial x}+\frac{\partial^2y(x)}{\partial x^2}=0———-(1)

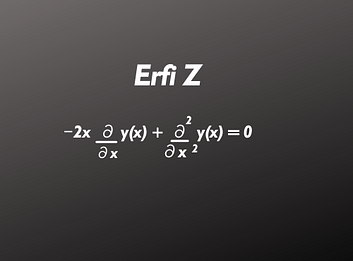
The initial condition of (1) at 0 is

erfi(0)=0

\;\frac{\partial erfi\;(x)}{\partial x}(0)={\textstyle\frac2{\sqrt\pi}}

Series and Asymptotic Expansions

2.1 Taylor expansion at 0.

2.1.1 First terms.

erfi\;(x)=\frac2{\sqrt\pi}x+\frac2{3\sqrt\pi}x^3+\frac1{5\sqrt\pi}x^5+\frac1{21\sqrt\pi}x^7+\frac1{108\sqrt\pi}x^9+\frac1{660\sqrt\pi}x^{11}+\frac1{4680\sqrt\pi}x^{13}+\frac1{37800\sqrt\pi}x^{15}+O(x^{16})

2.1.2 General form.

erfi(x)=\sum_{n=0}^\infty u(n)x^n

The coefficients u(n) satisfy the recurrence

-2nu(n)+(n2 + 3n+2)u(n+2)=0 —————(.2.1.2.2)

Initial conditions of 2.1.2.2 are given by

U(0)=0

U(1)=\frac2{\sqrt\pi}

Erf Imaginary Error Function for Floating-Point and Symbolic Numbers:

Depending on its logic, erf can return floating-point or exact symbolic results. Work out the imaginary error function for these numbers. Because these numbers are not symbolic objects, you get floating-point results.

s=\left[erfi(\frac12),erfi(1.41),\;erfi(\sqrt{2)}\right]

s=0.615\;\;\;\;\;\;\;\;3.7382\;\;\;\;\;\;3.7731

Evaluate the imaginary error function for the same numbers converted to symbolic objects. For most symbolic numbers, erf x returns undetermined symbolic calls.

Imaginary Error Function for Variables and Expressions:

Compute the imaginary error function for x and \;\sin(x)\;+\;x\ast e^x . For most symbolic variables and expressions, erfi x returns unresolved symbolic calls.

“Error Function”

In mathematics, the error function is also called the Gauss error function. often denoted by erf, is a complex function of a complex variable defined as

erf\; z = \frac2\pi\int_0^z\;e^{-t^2}\;dt.

This integral is a special function that occurs often in calculus. In calculus, a function argument is a real number. If the function argument is real, then the function value is also a real number.

Properties:

The property erf\;(-z)\;=\;-erf\;z\; means that the error function is an odd function. This directly results from the fact that the integrand e^{-t^2} is an even (integrating an even function gives an odd function and vice versa.

For complex number z :

erf\;\overline z\;=\overline{erf\;z}.

where \overline z\; is complex conjugate of z

for math, basic knowledge click here