HOMOGENEOUS EQUATION: Each equation of the system of following linear equations
![]() .
.
![]() .
.
![]() .
.
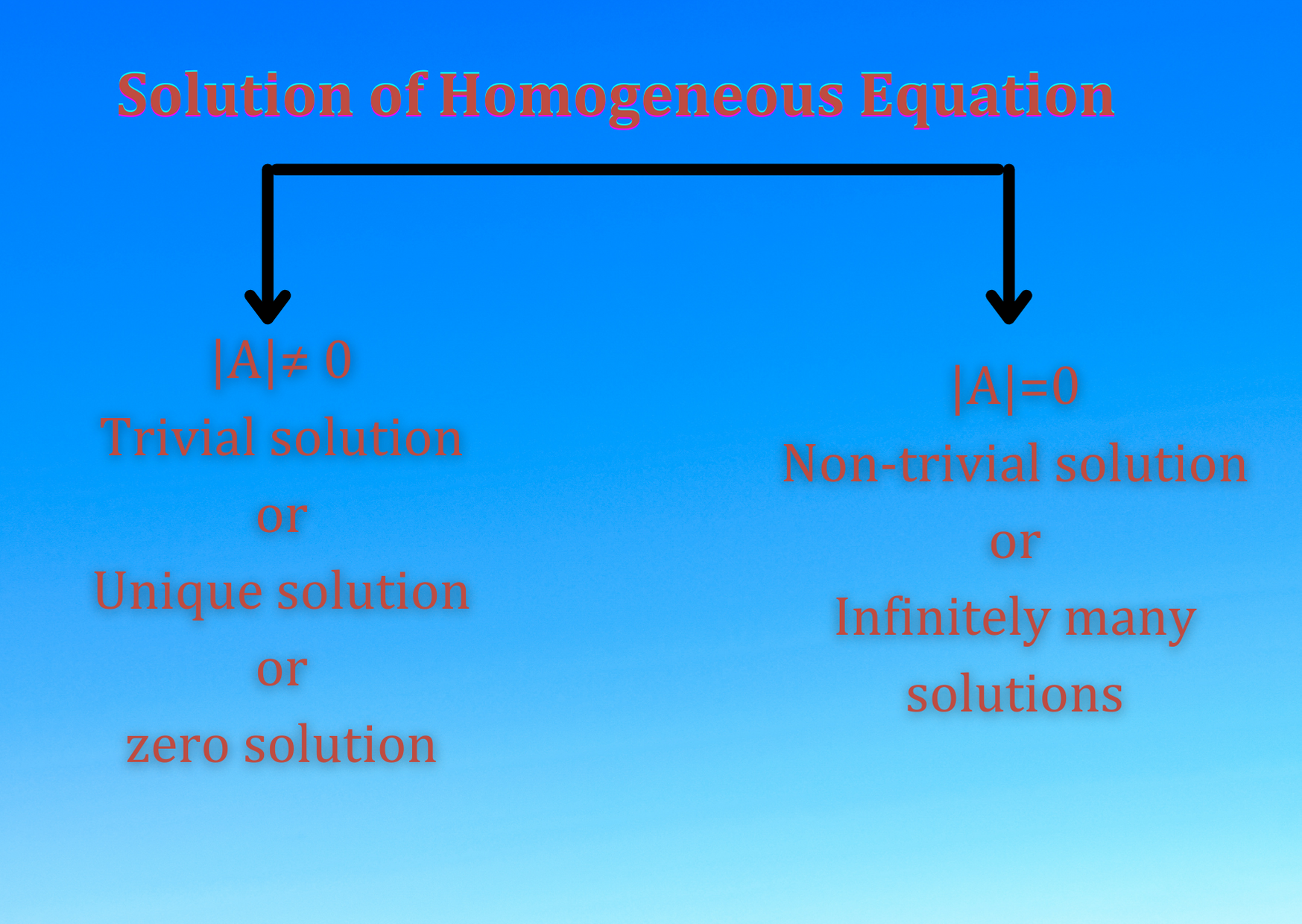
is always satisfied by ![]() , so such a system is always consistent. The solution
, so such a system is always consistent. The solution ![]() of the above homogeneous equations
of the above homogeneous equations ![]() is called the trivial solution. Any other solution of equations
is called the trivial solution. Any other solution of equations ![]() other than the trivial solution is called a non-trivial solution.
other than the trivial solution is called a non-trivial solution.
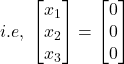
The above system can be written as
![]() where
where 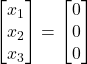
If ![]() , then
, then ![]() is non-singular and
is non-singular and ![]() exists, that is
exists, that is
![]()
![]()
![]()
 .
.
In this case the system of homogeneous equations possesses only the trivial solution.
Now we consider the case when the system has a non-trivial solution. Multiplying the equations ![]() and
and ![]() by
by ![]() and
and ![]() respectively and adding the resulting equations (where
respectively and adding the resulting equations (where ![]() and
and ![]() are cofactors of the corresponding elements of
are cofactors of the corresponding elements of ![]() ),
),
we have![]() .
.
that is,
![]() .
.
Similarly, we can get
![]()
For a non-trivial solution, at least one of ![]() and
and ![]() is different from zero
is different from zero
Let ![]() , then from
, then from ![]() ., we have
., we have ![]() .
.
For example, the system
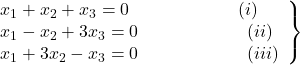 .
.
has a non-trivial solution because
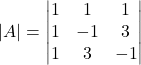
 .
.
by ![]() .
.
![]()
![]()
Adding ![]() , we get
, we get
![]()
![]()
And subtracting ![]() , we get
, we get
![]()
![]()
Putting ![]() and
and ![]() in (III), we see that
in (III), we see that ![]() , which shows that the equation
, which shows that the equation ![]() are satisfied by
are satisfied by
![]() for any real value of t.
for any real value of t.
Thus the system consisting of ![]() has infinitely many solutions.
has infinitely many solutions.
But the system
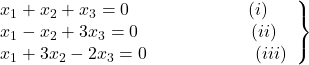 .
.
has only the trivial solution.
because in this case
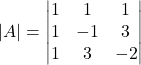
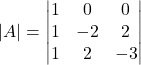 .
.
by ![]() .
.
![]() .
.
![]() .
.
Solving the first two equations of the above system, we get
![]() and
and ![]() .
.
Putting ![]() and
and ![]() in the expression
in the expression ![]()
we have,
![]() ,
,
that is, the third equation is not satisfied by putting
![]() and
and ![]()
But it is satisfied only if ![]() .
.
Thus the above system has only the trivial solution.
you can also check homogenous function.
