What is Homogeneous Function Definition:
A function ![]() defined by
defined by
![]()
of any number of variables are said to be homogeneous of degree ![]() in these variables if multiplication of these variables by any number
in these variables if multiplication of these variables by any number ![]() result in the multiplication of the function by
result in the multiplication of the function by ![]() .
.
![]()
provide that ![]() is in the domain of
is in the domain of ![]() .
.

Taking ![]() the equation
the equation![]() becomes
becomes
![]() .
.
![]() .
.
![]() .
.
which is another criterion for a function to be in a homogeneous function. so after the homogeneous function definition now come to the examples
Homogeneous Function Example: 1
consider the function ![]() defined by
defined by
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() .
.
Thus f is homogenous function of degree 0.
Homogeneous Function Example: 2
Let
![]() .
.
Here
![Rendered by QuickLaTeX.com f(x,y)=\frac{\sqrt y+\sqrt x}{y+x}=\frac{\sqrt x\left[1+\sqrt{\displaystyle\frac yx}\;\right]}{x\left[1+{\displaystyle\frac yx}\right]}](https://doublemath.com/wp-content/ql-cache/quicklatex.com-87b02f2d5a5e9bbf89dc3474272f4750_l3.png) .
.
![Rendered by QuickLaTeX.com f(x,y)=x^\frac{-1}2\frac{\left[1+\sqrt{\displaystyle\frac yx}\;\right]}{\left[1+{\displaystyle\frac yx}\right]}](https://doublemath.com/wp-content/ql-cache/quicklatex.com-b00a2aec8dfd920b85cbe0c1f61aa5ea_l3.png) .
.
Thus ![]() is a homogeneous function of degree
is a homogeneous function of degree ![]() .
.
Another Method:
Let
![]() .
.
Then
![]() .
.
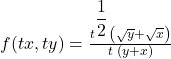
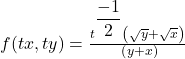 .
.
![]() .
.
Thus ![]() is a homogeneous function of degree
is a homogeneous function of degree ![]() .
.
also check homogeneous equation you can also see this topic from here
