Logarithmic Differentiation, 3 Examples with best solution

Leave a Comment / Mathematics / By Azhar

Logarithmic Differentiation: Let $f(x)=u^v$ where both $u$ and $v$ are variables or function of $x$ , the derivative of $f(x)$ can be obtained by taking natural logarithms of both of sides and the differentiating .

Example

This image has an empty alt attribute; its file name is 14.jpg

$f(x)=x^x$

$lnf(x)=ln(x^x)$

now by usning property of ln

$lnf(x)=x.lnx$

differentiate w.r.t x

$\frac d{dx}\ln f(x)=\frac d{dx}x.\ln x$

property of ln and product rule

$\frac1{f(x)}\frac d{dx}f(x)=\ln x\frac d{dx}x+x\frac d{dx}\ln x$

$\frac{f'(x)}{f(x)}=\ln x(1)+x\frac1x$

$\frac{f'(x)}{f(x)}=\ln x+1$

$f'(x)=f(x).\left(\ln x+1\right)$

$\boxed{f'(x)=x^x.\left(\ln x+1\right)}$

Example  derivative of lnx and graph

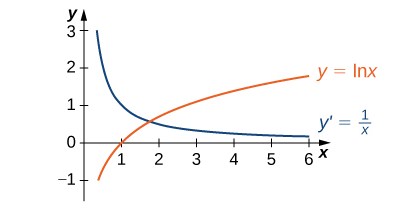
Logarithmic Differentiation

$f(x)=lnx$

differentiate w.r.t x

$\frac d{dx}f(x)=\frac d{dx}\ln x$

using ln property

$\boxed{f'(x)=\frac1x}$

Derivative of ln x (Logarithmic Differentiation)

Example  derivative of ln x power 2 and graph

Logarithmic Differentiation

$f(x)=\ln x^2$

differentiate w.r.t x

$\frac d{dx}f(x)=\frac d{dx}\ln x^2$

$f'(x)=\frac1{x^2}\frac d{dx}x^2$

$f'(x)=\frac1{x^2}2x$

$\boxed{f'(x)=\frac2x}$

This is required derivative of ln of x square.

Example derivative of ln(sinx) and graph

$y=\ln(\sin x)$

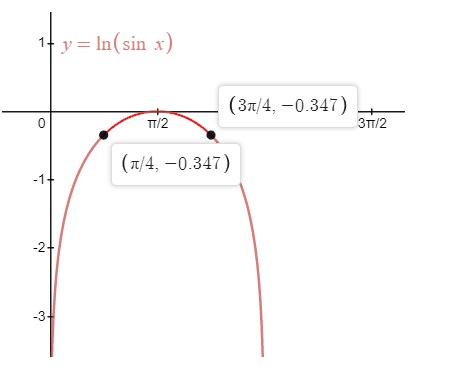
differentiate w.r.t x

$\frac d{dx}y=\frac d{dx}\ln(\sin x)$

$\frac d{dx}y=\frac1{\sin x}.\frac d{dx}(\sin x)$

$\frac d{dx}y=\frac1{\sin x}.\cos x$

$\boxed{\frac d{dx}y=cotx}$

Leave a Comment Cancel Reply