Power Series Expansion

A series of the from $a_0 + a_1x +a_2 x^2 +a_3 x^3 +.......+a_n x^n+.........$ is called power series expansion of a function $f(x)$ , where $a_0 , a_1, a_2, a_3,.....,a_n,....$ are constants and $x$ is variable.

Mathematics Of Power Series Expansion:

In order to explore power series we have to recall that the sum of a geometric series can be expressed using the simple formula:

$\sum_{n=0}^\infty kx^n=\frac k{1-x}$

If $|x|<1,$ , and that the series diverges when $|x|\geq1$ . At the time, we thought of $x$ as an unspecified constant, but we could just as well think of it as a variable, in which case the series

$\sum_{n=0}^\infty kx^n$

is a function, namely, the function $k/(1-x),$ as long as $|x|<1:$ Looking at this from the opposite perspective, this means that the function $k/(1-x)$ can be represented as the sum of an infinite series? Why would this be useful? While $k/(1-x)$ is a reasonably easy function to deal with, the more complicated representation $\sumkx^n$ does have some advantages: it appears to be an infinite version of one of the simplest function types — a polynomial. Later on, we will investigate some of the ways we can take advantage of this ‘infinite polynomial’ representation, but first, we should ask if other functions can even be represented this way.

The geometric series has a special feature that makes it unlike a typical polynomial—the coefficients of the powers of $x$ are all the same, namely $k$ . We will need to allow more general coefficients if we are to get anything other than the geometric series.

Power Series Centred Around Zero.

A power series is a series of the form

$P(x)= \sum_{n=0}^\infty a_n x^n$

where the coefficients $a_n$ are real numbers

Note:

As we did in the section on sequences, we can think of the anan as being a function a(n)a(n) defined on the non-negative integers.
It is important to remember that the anan do not depend on x.

Power Series Convergence.

Practice 1: Determine the values of $x$ for which the power series $\sum_{n=1}^\infty\frac{x^n}n$ converges.

Solution:

We can investigate convergence using the Ratio Test: $\lim_{x\rightarrow\infty}\frac{\left|x\right|^{n+1}}{n+1}\frac n{\left|x\right|^n}= \lim_{x\rightarrow\infty}\left|x\right| \frac n{n+1}=\left|x\right|$

Thus when $|x|<1$ the series converges and when $|x|>1|$ it diverges, leaving only two values in doubt. When $x=1$ the series is the harmonic series and diverges; when $x=-1$ it is the alternating harmonic series (actually the negative of the usual alternating harmonic series) and converges. Thus, we may think of $\sum_{n=1}^\infty\frac{x^n}n$ as a function from the interval [−1,1) to the real numbers.

\lim_{n\rightarrow\infty}\frac{\left|a_{n+1}\right|\left|x\right|^{n+1}}{\left|a_n\right|\left|x\right|^n}=\underset{n\rightarrow\infty}{\lim\;\left|x\right|}\frac{\left|a_{n+1}\right|}{\left|a_n\right|}=\underset{n\rightarrow\infty}{\left|x\right|\lim\;}\frac{\left|a_{n+1}\right|}{\left|a_n\right|}=L\left|x\right|

assuming that lim $\frac{\left|a_{n+1}\right|}{\left|a_n\right|}$

If L∈(0,∞):
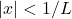- Then the series converges if $L\left|x\right|<1$ , that is, if $|x|<1/L$ , and diverges if $|x|>1/L$ .
- Only the two values 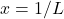$x=\pm1/L$ require further investigation.
- The value 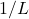$1/L$ is called the radius of convergence .
- Thus the series will always define a function on the interval 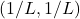$(-1/L,1/L)$ ,that perhaps will extend to one or both endpoints as well.
- This interval is referred to as the interval of convergence.
- This interval is essentially the domain of the power series .
If L=0:
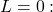
- Then no matter what value 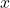$x$ takes the limit is 0.
- The series converges for all 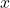$x$ and the function is defined for all real numbers.
If L=∞:
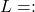
- Then no matter what value xx takes the limit is infinite.
- The series converges only when $x=0$ .

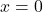We can make these ideas a bit more general. Consider the series

$\sum_{n=0}^\infty\frac{\left(x+2\right)^n}{3^n}$

This looks a lot like a power series, but with $(x+2)^n$ instead of $x^n$ . Let’s try to determine the values of xx for which it converges. This is just a geometric series, so it converges when

$\frac{\left|x+2\right|}3<1$

$\left|x+2\right|<3$

$-3<x+2<3$

$-5<x<1$

So the interval of convergence for this series is $(-5,1)$ . The centre of this interval is at $-2$ , which is at distance $3$ from the endpoints, so the radius of convergence is $3$ , and we say that the series is centred at $-2$ .

Interestingly, if we compute the sum of the series we get:

$\sum_{n=0}^\infty\left(\frac{x+2}3\right)^n=\frac1{1-{\displaystyle\frac{x+2}3}}=\frac3{1-x}$

Multiplying both sides by $1/3$ we obtain

$\sum_{n=0}^\infty\frac{\left(x+2\right)^n}{3^{n+1}}=\frac1{1-x}$

which we recognize as being equal to

$\sum_{n=0}^\infty x^n$

so we have two series with the same sum but different intervals of convergence.

This leads to the following definition:

Power Series Centred Around a:

Power series centered at $a$ has

P(x)=\sum_{n=0}^\infty a_n(x-a)^n

where the centre $a$ and coefficients katex]a_n[/katex] are real numbers.

Practice 2: Interval of Convergence

Given the power series

$\sum_{n=0}^\infty\frac{\left(-1\right)^nn\left(x-2\right)^n}{3^n}$

determine the following:

radius of convergence
interval of convergence

Solution:

Obviously, the series converges for $x=2$ . To determine all values of $x$ for which the series converges, we begin by applying the Ratio Test:

$L=\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_n}\right|$

$L=\lim_{n\rightarrow\infty}\left|\frac{\left(-1\right)^{n+1}(n+1)(x-2)^{n+1}}{3^{n+1}}\frac{3^n}{\left(-1\right)^nn(x-2)^n}\right|$

$L=\lim_{n\rightarrow\infty}\left|\frac{(n+1)(x-2)}{3n}\right|$

$L=\left|x-2\right|\lim_{n\rightarrow\infty}\frac{n+1}{3n}$

$L=\frac13\left(x-2\right)$

By the Ratio Test, the radius of convergence is $R=3$
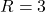
We now determine the interval of convergence. By the Ratio Test, the series converges absolutely if $L<1:$

$\frac13\left|x-2\right|<3$

$\Rightarrow\left|x-2\right|<3$

$\Rightarrow-3<x-2<3$

$\Rightarrow-1<x<5$

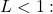
The series diverges if $L>1$ , i.e. $x<-1 and x>5$ . Let us now look at the case when $L=1$ , which means investigating the behaviour of the series at endpoints $x=-1 and x=5$ :

Case $x=-1$ : Then the series becomes

\sum_{n=0}^\infty\frac{\left(-1\right)^nn\left(1-1-2\right)^n}{3^n}=\sum_{n=0}^\infty\left(-1\right)^{2n}n=\sum_{n=0}^\infty n

Since , $\lim_{n\rightarrow\infty}n=\infty$ ≠0 this series is divergent by the $n-th$ Term Test (Divergence Test).

Case $x=5$ : Then the series becomes

\sum_{n=0}^\infty\frac{\left(-1\right)^nn\left(5-2\right)^n}{3^n}=\sum_{n=0}^\infty\left(-1\right)^nn

Since $\lim_{n\rightarrow\infty}\left(-1\right)^nn$ does not exist, this series is also divergent by the $n-th$ Term Test (Divergence Test).Thus, the interval of convergence for the given power series is $x\in(-1,5)$ .

Practice 2:

Interval of Convergence.

Given the power series

\sum_{n=1}^\infty(n+1)!(x+3)^n

determine the following:

radius of convergence
interval of convergence