Quadratic Formula Derivation: Again there are some quadratic polynomials that are not factorable at all using integral coefficients. In such a case we can always find the solution of a quadratic equation by the quadratic formula.
a x^2+bx+c = 0 by applying a formula known as the quadratic formula. This formula is applicable for every quadratic equation.
- Derivation of Quadratic Formula
The standard form of a quadratic equation is
ax^2+bx + c = 0, \;\;\;\;\;\;\;\;\;\;\;\;;a ≠ 0
Step 1. Divide the equation by a
x^2+\frac bax+\frac ca=0
Step 2. Take constant term to the R.H.S
x^2+\frac bax=-\frac ca
Step 3. To complete the square on the L.H.S. add {(\frac b{2a})}^2 to both sides
x^2+\frac bax+\frac{b^2}{4a^2}=\frac{b^2}{4a^2}-\frac ca
(x+\frac b{2a})^2=\frac{b^2-4ac}{4a^2}
(x+\frac b{2a})=\pm\frac{\sqrt{b^2-4ac}}{2a}
x=-\frac b{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
Hence the solution of the quadratic equation ax^2+bx + c = 0 is given by
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}
which is called Quadratic formula.
- Example 1: Solve the equation 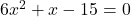6x^2 +x - 15 = 0 by using the quadratic formula.
Solution:
Comparing the given equation with
ax^2+bx + c = 0,
we get,
,a = 6, b = 1, c = - 15,
∴ The solution is given by
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a},
x=\frac{-1\pm\sqrt{1^2-4(6)(-15)}}{2(6)},
,x=\frac{-1\pm\sqrt{361}}{12},
x=\frac{-1\pm19}{12}
,i.e,\;\;\;\;\;\;\;\;\; x=\frac{-1+19}{12} \;\;\;\;\;\;\;\;\;or \;\;\;\;\;\;\;\;\; x=\frac{-1-19}{12},
- Example 2: Solve the equation 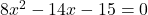8x^2 -14x - 15 = 0 by using the quadratic formula.
Solution:
Comparing the given equation with
ax^2+bx + c = 0,
we get,
,a = 8, b = -14, c = - 15,
∴ The solution is given by
x=\frac{-b\pm\sqrt{b^2-4ac}}{2a},
x=\frac{-(-14)\pm\sqrt{(-14)^2-4(8)(-15)}}{2(8)},
,x=\frac{14\pm\sqrt{676}}{16},
x=\frac{14\pm26}{16},
,i.e,\;\;\;\;\;\;\;\;\; x=\frac{14+26}{16} \;\;\;\;\;\;\;\;\;or \;\;\;\;\;\;\;\;\; x=\frac{14+26}{16},
you can also check from.