
Rolle’s Theorem Statement: let a function ![]() be
be
- Continuous on the interval
![Rendered by QuickLaTeX.com \left[a\;,\;b\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-f2e2bbf65b666d2fd31d89a08819946d_l3.png) .
. - Differentiable on the open interval
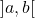 .
. 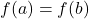
then there exist at least one point ![]() such that
such that ![]() .
.
Proof:
since ![]() is contineous on
is contineous on ![]() , it is bounded their attains its bounds.
, it is bounded their attains its bounds.
Let ![]() and
and ![]() be the supremum and infimum of
be the supremum and infimum of ![]() on
on ![]() .
.
then their either ![]() or
or ![]()
If ![]() then the funtion is constant on
then the funtion is constant on ![]() so its derivatives vanishes at each point of the interval.
so its derivatives vanishes at each point of the interval.
Hence the theorem is true in this case.
If ![]() at least one of them is different from the equal values
at least one of them is different from the equal values ![]() and
and ![]() .
.
Suppose ![]()
Since ![]() attains its supremum on
attains its supremum on ![]() , there is a point
, there is a point ![]() such that
such that ![]() , But then because of
, But then because of ![]() must be diffrent from
must be diffrent from ![]() and
and ![]() . Thus
. Thus ![]() .
.
Let ![]() be a positive real number such that
be a positive real number such that ![]() and
and ![]() both lie in
both lie in ![]() . Then
. Then
![]()
and ![]()
Since ![]() on
on ![]() .
.
Hence
![]()
and
![]()
![]()
Taking ![]() , we obtain from
, we obtain from ![]() and
and ![]()
![]()
showing that ![]() .
.
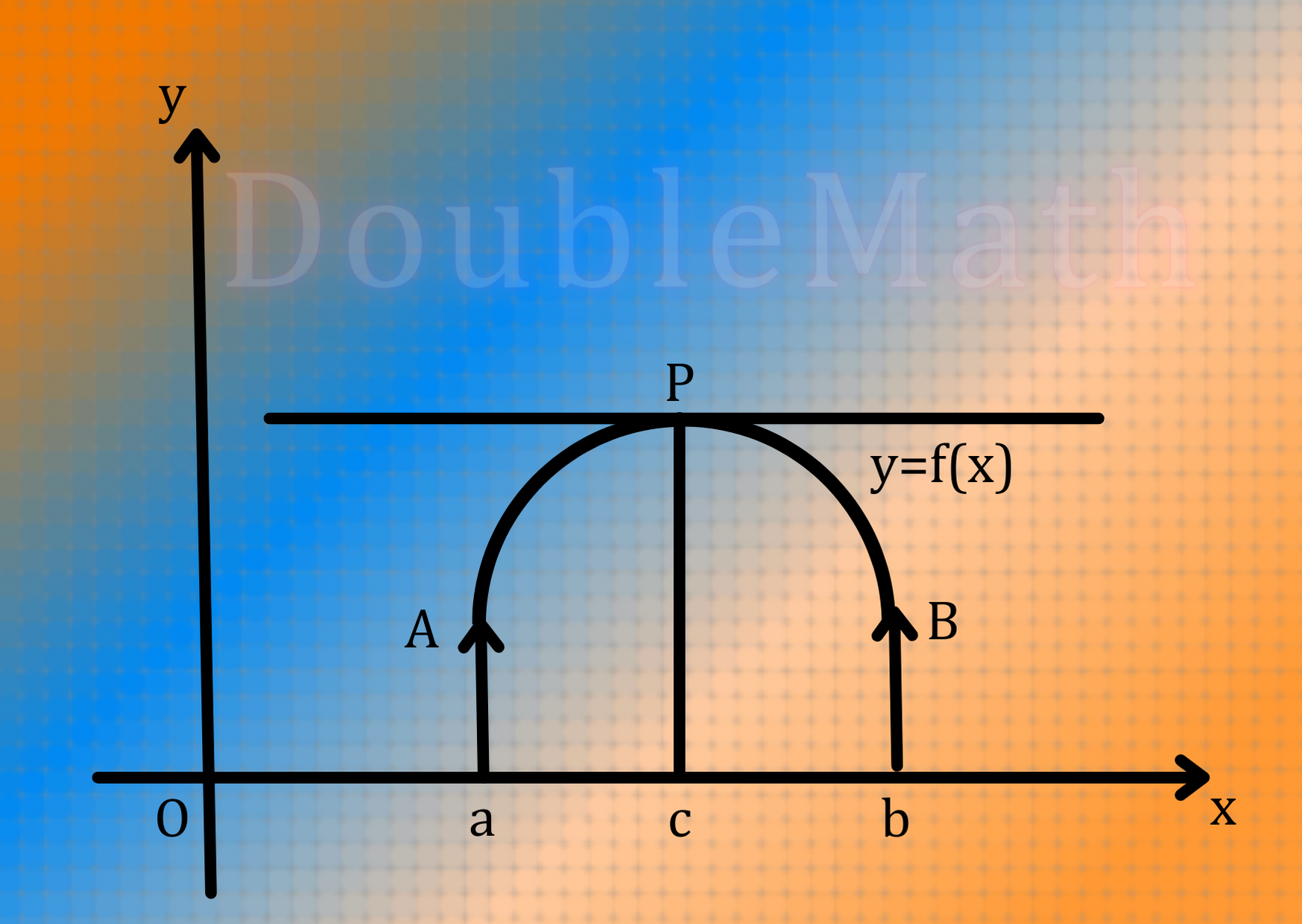
Geometrical Interpretation of Rolle’s Theorem:
Rolle’s Theorem has a simple geometrical interpretation. If f is contineous on ![]() and Differentiable on the open interval
and Differentiable on the open interval ![]() such that
such that ![]() then there is a point
then there is a point ![]() where the tangent line to the graph of
where the tangent line to the graph of ![]() is parallel to the
is parallel to the ![]() . There may be more then one point on the graph where the tangent lines are parallel to the
. There may be more then one point on the graph where the tangent lines are parallel to the ![]() as in figure.
as in figure.
for physical illustration of Rolles theorem, let a stone by thrown by the ground into the air. Suppose the Hight of the stone after time ![]() is
is ![]() The stone will hit the ground after some time
The stone will hit the ground after some time ![]() . Then clearly
. Then clearly ![]() the function
the function ![]() satisfies the condition of Rolles Theorem on the interval
satisfies the condition of Rolles Theorem on the interval ![]() . Hence the certain
. Hence the certain ![]() , the velocity of the stone is zero
, the velocity of the stone is zero ![]() . We know that it indeed happens.
. We know that it indeed happens.
Example:
Verify Rolles Theorem for
![]() on
on ![]()
Solution:
If ![]() is continuous on
is continuous on ![]() and
and ![]()
![]()
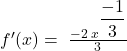
Thus ![]() intermediate and so
intermediate and so ![]() is not differentiable at
is not differentiable at ![]() .
.
Hence Rolles Theorem fail for the given condition.
