What is Parabola: If the intersecting plane is parallel to the generator of the cone but cut only one nappe is called parabola. We have already stated that a conic section is a parabola if e = 1. Here e is the eccentricity.
We shall first derive an equation of a parabola in standard form and study its important properties.
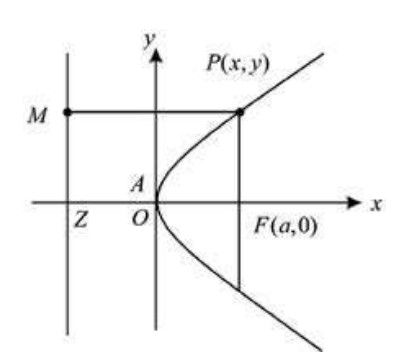
If we take the focus of the parabola as F (a, 0),\;a > 0 and its directrix as line L whose equation is x = -a, then its equation becomes very simple. Let P(x, y) be a point on the parabola.
So, by definition
\frac{\left|PF\right|}{\left|PM\right|}=1 \;\;\;\;or\;\;\;\; \left|PF\right|=\left|PM\right|
Now,
\left|PM\right|=x+a\;\;\;\;\;\;\;\;(1)
\left|PF\right|=\sqrt{(x-a)^2+(y-0)^2}
Substituting into (1), we get
\sqrt{(x-a)^2+(y-0)^2}=x+a
(x-a)^2+(y)^2=(x+a)^2
y^2=(x+a)^2-(x-a)^2
y^2=4ax
which is standard equation of Parabola
Some Definitions:
what is parabola
- The line through the focus and perpendicular to the directrix is called axis of parabola. In case of (2), the axis is y = 0.
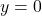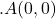- The point where the axis meets the parabola is called vertex of parabola. Clearly the equation (2) has vertex .A(0,0).. The line through A and perpendicular to the axis of the parabola has equation 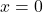x = 0.. It meets the parabola at coincident points and so it is a tangent to the curve at A.
- A line joining two distinct points on a parabola is called a chord of parabola. A chord passing through the focus of a parabola is called a focal chord of parabola. The focal chord perpendicular to the axis of the parabola 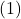(1) is called latusrectum of parabola. It has an equation x = a and it intersects the curve at the points where
y^2 = 4a^2 \;\;\;\;\;or\;\;\;\;\; y+\pm 2a
Thus coordinates of the end points L and L’ of the latusrectum are
L(a ,2a )\;\;\;\;\;\; and\;\;\;\;\; L'(a ,- 2a ).
The length of the latusrectum is \left|LL'\right|=4a
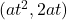- The point (at^2 , 2at) lies on the parabola [/latex]y^2=4ax[/latex] for any real t.
x = at^2 \;\;\;\;\;\;\;\;\;,y = 2at
are called parametric equations of parabola y^2 = 4ax