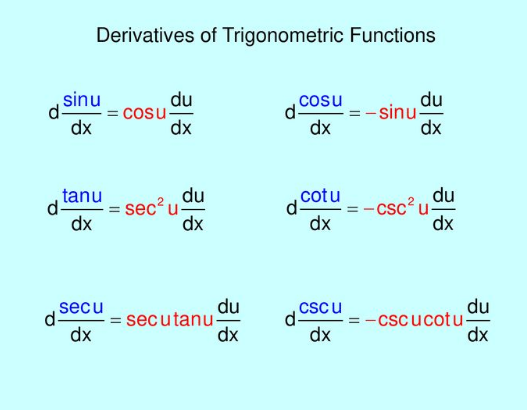
Derivative of Trigonometric functions
Here will will discuss Derivative of sinx, cosx, tanx, cosecx, secx and cotx functions.
Derivative of sinx function
![]()
![]()
![]()
![]()
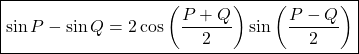
![]()
![]()
dividing ![]() on both sides.
on both sides.
![]()
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\displaystyle\delta y}{\displaystyle\delta x}=\underset{\delta x\rightarrow0}{lim}\left[2\frac{\displaystyle\cos\left(\frac{\displaystyle2x+\delta x}{\displaystyle2}\right)\sin\left(\frac{\displaystyle\delta x}{\displaystyle2}\right)}{\displaystyle\delta x}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-20d70f638b658b6a19b7a2b1a19011df_l3.png)
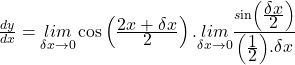
![]()
as we know 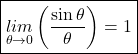
![]()
![]()
This is the required derivative of sinx.
Derivative of cosx function
![]()
![]()
![]()
![]()
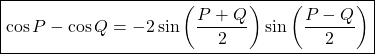
![]()
![]()
dividing ![]() on both sides.
on both sides.
![]()
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\displaystyle\delta y}{\displaystyle\delta x}=\underset{\delta x\rightarrow0}{lim}\left[2\frac{\displaystyle-sin\left(\frac{\displaystyle2x+\delta x}{\displaystyle2}\right)\sin\left(\frac{\displaystyle\delta x}{\displaystyle2}\right)}{\displaystyle\delta x}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-ec7b93f548cb20e0d91599eefcd5ef43_l3.png)
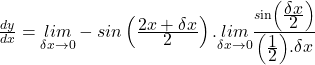
![]()
As we know 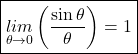
![]()
![]()
This is the required derivative of cosx.
Derivative of Tanx function
![]()
![]()
![]()
![]()
![]()
![]()
using formula:
![]()
![]()
![]()
dividing ![]() on both sides.
on both sides.
![]()
Taking ![]() on both sides.
on both sides.
![]()
![]()
![]()
As we know 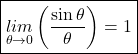
![]()
![]()
This is the required derivative of tanx.
Derivative of Cosecx function
![]()
![]()
![]()
![]()
![]()
![]()
using formula
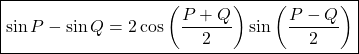
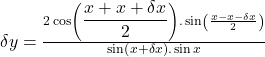
dividing ![]() on both sides.
on both sides.
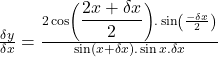
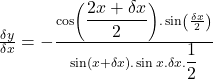
Taking ![]() on both sides.
on both sides.
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\delta y}{\delta x}=-\underset{\delta x\rightarrow0}{lim}\left[\frac{\cos\left({\displaystyle\frac{2x+\delta x}2}\right).\sin\left(\frac{\delta x}2\right)}{\sin\left(x+\delta x\right).\sin x.{\displaystyle\frac{\delta x}2}}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-bdbe740635aa79b8797939878e459dfc_l3.png)
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\delta y}{\delta x}=-\underset{\delta x\rightarrow0}{lim}\left[\frac{\cos\left({\displaystyle\frac{2x+\delta x}2}\right)}{\sin\left(x+\delta x\right).\sin x.}\right]\underset{\delta x\rightarrow0}{.lim}\left[\frac{\sin\left(\frac{\delta x}2\right)}{\frac{\delta x}2}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-df3de2a7e900f589d695a8094057eff9_l3.png)
now using formula 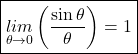
![Rendered by QuickLaTeX.com \frac{dy}{dx}=-\left[\frac{\cos\left({\displaystyle\frac{2x+0}2}\right)}{\sin\left(x+0\right).\sin x.}\right].1](https://doublemath.com/wp-content/ql-cache/quicklatex.com-a9ce60423a34662befef386892302090_l3.png)
![]()
![]()
![]()
This is the required derivative of cosecx.
Derivative of secx function
![]()
![]()
![]()
![]()
![]()
![]()
using formula
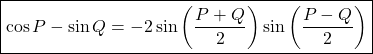
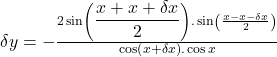
dividing ![]() on both sides.
on both sides.
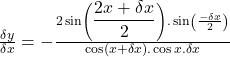
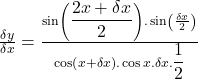
Taking ![]() on both sides.
on both sides.
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\delta y}{\delta x}=\underset{\delta x\rightarrow0}{lim}\left[\frac{\sin\left({\displaystyle\frac{2x+\delta x}2}\right).\sin\left(\frac{\delta x}2\right)}{\cos\left(x+\delta x\right).\cos x.{\displaystyle\frac{\delta x}2}}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-61e948362ac29dbf990b59ea3972024f_l3.png)
![Rendered by QuickLaTeX.com \underset{\delta x\rightarrow0}{lim}\frac{\delta y}{\delta x}=-\underset{\delta x\rightarrow0}{lim}\left[\frac{\sin\left({\displaystyle\frac{2x+\delta x}2}\right)}{\cos\left(x+\delta x\right).\sin x.}\right]\underset{\delta x\rightarrow0}{.lim}\left[\frac{\cos\left(\frac{\delta x}2\right)}{\frac{\delta x}2}\right]](https://doublemath.com/wp-content/ql-cache/quicklatex.com-dbd5c7bf13e191e17060ff420b7af5c2_l3.png)
now using formula 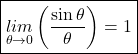
![Rendered by QuickLaTeX.com \frac{dy}{dx}=-\left[\frac{\cos\left({\displaystyle\frac{2x+0}2}\right)}{\sin\left(x+0\right).\sin x.}\right].1](https://doublemath.com/wp-content/ql-cache/quicklatex.com-a9ce60423a34662befef386892302090_l3.png)
![]()
![]()
![]()
This is the required derivative of secx.
Derivative of Cotx function
![]()
![]()
![]()
![]()
![]()
![]()
using formula:
![]()
![]()
![]()
dividing ![]() on both sides.
on both sides.
![]()
Taking ![]() on both sides.
on both sides.
![]()
![]()
![]()
As we know 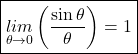
![]()
![]()
This is required derivative of cotx. (derivative of trigonometric functions)
