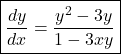 Implicit Differentiation:
Implicit functions: If y and x are mixed up and y cannot be expressed in terms of the independent variable x, Then y is called an Implicit functions. Symbolically it is written as f\left(x,y\right)=0
Examples:
x^3+xy-x=7
y^3+xy-x=0
y^3+xy-xy^3=0
Procedure:
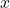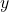- Step (1) when x and y are related Implicit we assumethat 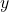y is differentiable function of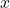 x
- Step (2) Differentiate both sides of eq w.r.t x
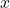
- Step (3) Solve the resulting eq for \frac{dy}{dx}
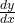
Example 1: Implicit Differentiation
x^3+xy-x=7
Differentiate w.r.t x
\frac d{dx}\left(x^3+xy-x\right)=\frac d{dx}7
\frac d{dx}\left(x^3\right)+\frac d{dx}\left(xy\right)-\frac d{dx}(x)=\frac d{dx}7 [sum and difference rule]
3x^2+\left[y\frac d{dx}x+x\frac d{dx}y\right]-1=0
3x^2+y+x\frac d{dx}y=1
x\frac d{dx}y=1-3x^2-y
\boxed{\frac d{dx}y=\frac{1-3x^2-y}x}
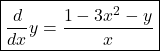
Example 2: [implicit Differentiation]
y^3+xy-x=0
Differentiate w.r.t x
\frac d{dx}\left(y^3+xy-x\right)=\frac d{dx}0
\frac d{dx}y^3+\frac d{dx}xy-\frac d{dx}x=\frac d{dx}0 [sum and difference rule]
3y^2+y\frac d{dx}x+x\frac d{dx}y-1=0
3y^2+y+x\frac d{dx}y=1
x\frac d{dx}y=1-3y^2-y
\boxed{\frac d{dx}y=\frac{1-3y^2-y}x}
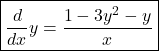
Example 3: [implicit Differentiation]
y^3+y-xy^3=0
Differentiate w.r.t x
\frac d{dx}\left(y^3+y-xy^3\right)=\frac d{dx}0
\frac d{dx}y^3+\frac d{dx}y-\frac d{dx}xy^3=0 [sum and difference rule]
3y^2+\frac d{dx}y-\left[y^3\frac d{dx}x+x\frac d{dx}y^3\right]=0
3y^2+\frac d{dx}y-\left[y^3+3xy^2\frac{dy}{dx}\right]=0
3y^2+\frac d{dx}y-y^3-3xy^2\frac{dy}{dx}=0
\frac d{dx}y-3xy^2\frac{dy}{dx}=y^3-3y^2
\frac d{dx}\left(y-3xy^2\right)=y^3-3y^2
\frac{dy}{dx}=\frac{y^3-3y^2}{y-3xy^2}
\frac{dy}{dx}=\frac{y\left(y^2-3y\right)}{y(1-3xy)}
\boxed{\frac{dy}{dx}=\frac{y^2-3y}{1-3xy}}