As a three-dimensional geometrical shape (rectangle) a rectangular prism can be defined as
It’s 3D three-dimensional figure with six rectangular faces. Six rectangular faces make up a solid (3-dimensional) object. Moreover, its cross-section remains the same along its length, making it a prism. A cuboid is another name for a rectangular prism.
What is a Rectangular Prism?
Prisms with rectangular bases, which are rectangular on both sides, are known as rectangular prisms. In a rectangular prism, all the opposite faces are identical because it has six opposite faces, i.e., there are three pairs of identical opposite faces. In addition to its length, width, and height, it has three dimensions. Rectangular prisms can be found in a variety of objects in real life, including tissue boxes, notebooks, laptops, fish tanks, and large structures like cargo containers, rooms, or storage sheds.
How many faces and Vertices does a rectangular Prism have?
Prism has 6 faces, 12 edges, and 8 vertices. a right angle is formed at each vertex by three edges intersecting.
Formulas For Rectangular Prism
As we proceed through this section, we will learn about the volume and surface area of a rectangular prism. Consider a rectangle with dimensions ‘l’, ‘w’, and ‘h’ for both of these problems. We have assumed that the base’s dimensions are ‘l’ and ‘w’. A rectangular prism’s volume and surface area can be calculated using these formulas.
Volume = lwh
Total surface area=2(lw+wh+hl)
Lateral surface area=2(wh+hl)
Write the definitions of faces, vertices, and edges?
The term face refers to a flat surface. Face edges are the points where two faces meet. An intersection of two or more edges is referred to as a vertex. Vertices are plural forms of vertices.
Volume of Rectangular Prism
Rectangular prisms have a volume equal to the space they occupy. By multiplying a prism’s base area by its height, we can calculate its volume.
- The base area of the rectangular prism =
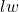 (using the area of a rectangle formula)
(using the area of a rectangle formula) - The height of the rectangular prism =
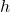
- volume of the rectangular prism, V =
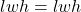 .
.
Surface Area of Rectangular Prism
There are two types of surface areas of a rectangular prism, Total surface area
Lateral surface area .
- All the faces of a rectangular prism add up to make its total surface area.
- All the side faces (excluding the bases) of a rectangular prism contribute to its lateral surface area.
We can calculate the areas of the side faces of a rectangular prism using its net.
The total surface area of a rectangular prism
= The sum of areas of all faces
=![]() .
.
=![]() .
.
Lateral surface area
= The sum of areas of side faces
=![]() .
.
=![]() .
.
