Order of a Group: The order of group ![]() is the number of elements present in that group
is the number of elements present in that group ![]() , also say it’s cardinality. It is denoted by
, also say it’s cardinality. It is denoted by ![]() or
or ![]() .
.
Examples:

- Dihedral group
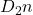 has order
has order 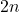
- Symmetric group
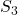 has order
has order 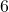
 ={
={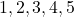 } modulo
} modulo 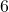 has order
has order 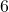 .
.
Order of an element:
Order of element ![]() is the smallest positive integer
is the smallest positive integer ![]() such that
such that ![]() , where
, where ![]() denotes the identity element of the group, and
denotes the identity element of the group, and ![]() denotes the product of
denotes the product of ![]() copies of
copies of ![]() The order of every element of a finite group is finite.
The order of every element of a finite group is finite.
- The Order of an element
 of group is the same as that of its inverse
of group is the same as that of its inverse 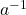 .
. - If
 is an element of order
is an element of order 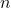 and
and  is prime to
is prime to 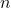 , then
, then 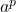 is also of order
is also of order 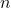 .
. - Order of any integral power of an element
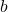 cannot exceed the order of
cannot exceed the order of 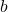 .
. - If the element
 of a group
of a group  is of order
is of order 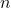 , then
, then 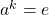 if and only if
if and only if 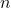 is a divisor of
is a divisor of 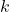 .
. - The order of the elements
 and
and 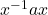 is the same where
is the same where  are any two elements of a group.
are any two elements of a group. - If
 and
and 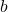 are elements of a group then the order of
are elements of a group then the order of 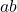 is same as order of
is same as order of 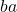 .
.
Cosets of subgroup H in group G:
Let ![]() be a subgroup of a group
be a subgroup of a group ![]() . If
. If ![]() , the right coset of
, the right coset of ![]() generated by
generated by ![]() is,
is, ![]() = {
= { ![]() };
};
and similarly, the left coset of ![]() generated by
generated by ![]() is
is ![]() = {
= { ![]() }
}
Example:
Consider ![]() under addition
under addition ![]() , and let
, and let ![]() is identity element. Find the left cosets of
is identity element. Find the left cosets of ![]() ?
?
Solution:
The left cosets ofin
are,
| Hence there are two cosets, namely |
