The history of mathematics shows that man has been developing and enlarging his concept of number according to the saying that “Necessity is the mother of invention”.
In the remote past they stared with the set of counting numbers and invented, by stages, the rational numbers, negative numbers, irrational numbers. Since square of a negative as well as positive number is a positive number and the square root of a negative number does not exist in the real numbers. So, square roots of negative numbers were given no attention for centuries together.
The numbers of the form x + iy, where x, y and i = ,are called complex numbers, here x is called real part and y is called imaginary part of the complex number. For example, [katex]2+5\imath , 3-\imath[/katex] etc. are complex numbers.
Important note about complex number
Every real number is a complex number with 0 as its imaginary part (note).
Now , start with considering the equation.
[katex]x^{2}+1=0 \newline \Rightarrow x^{2} \, =-1\newline\Rightarrow x = \pm 1[/katex]
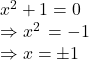
Which does not belong to the set of real numbers. Therefore we, for convenience call it imaginary number and denote it by [katex]\imath[/katex] (read as iota).
The product of a real number and i(iota) is also an imaginary number
Thus 7[katex]\imath[/katex], -5[katex]\imath[/katex], 5[katex]\imath[/katex] , [katex]\imath[/katex] are all imaginary numbers, [katex]\imath[/katex] which may be written 1.[katex]\imath[/katex] is also an imaginary number.
Powers of i :
[katex]i^{2}= -1\newline i^{3}= i^{2}.i=-1.i=-i \newline i^{4}=i^{2}i^{2}=-1.-1=1[/katex]
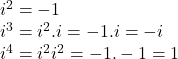
Therefore any power of i equal to 1, i,-1 or -i.