Sum and Difference Rule of Derivatives

Sum and difference rule of derivative

Theorem:

Let $f$ and $g$ are differentiable at $x$ ,

Then ( $f+g$ ) and ( $f-g$ ) are also differentiable at $x$ and

$\left[f\left(x\right)+g\left(x\right)\right]'=f'\left(x\right)+g'\left(x\right)$

That is

$\frac d{dx}\left[f\left(x\right)+g\left(x\right)\right]=\frac d{dx}\left[f\left(x\right)\right]+\frac d{dx}\left[g\left(x\right)\right]$

also

$\left[f\left(x\right)-g\left(x\right)\right]'=f'\left(x\right)-g'\left(x\right)$

That is

$\frac d{dx}\left[f\left(x\right)-g\left(x\right)\right]=\frac d{dx}\left[f\left(x\right)\right]-\frac d{dx}\left[g\left(x\right)\right]$

Proof

You can prove sum and difference derivatives in easy way by using following pattren.
Step 1:    Let function
Step 2:    adding  and  in  and  component respectively 
Step 3:  Subtracting 
Step 4:  Dividing  on both sides.
Step 5:  applying  on both sides.

Step 1:

Let $ϕ(x)=f(x)+g(x)..............(1)$

Step 2:    Adding  on both sides

$\phi(x+\delta x)=f(x+\delta x)+g(x+\delta x)..........(2)$

Step 3: Subtracting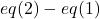

$\phi(x+\delta x)-\phi(x)$

$=\left[f(x+\delta x))+g(x+\delta x)\right]-\left[f(x)+g(x)\right]$

$\phi(x+\delta x)-\phi(x)=f(x+\delta x)+g(x+\delta x)-f(x)-g(x)$

$\phi(x+\delta x)-\phi(x)=[f(x+\delta x)-f(x)]+[g(x+\delta x)-g(x)]$

Step 4: Dividing 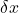 on both sides

$\frac{\phi(x+\delta x)-\phi(x)}{\delta x}=\frac{\lbrack f(x+\delta x)-f(x)\rbrack}{\delta x}+\frac{\lbrack g(x+\delta x)-g(x)\rbrack}{\delta x}$

Step 5: Taking 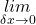 on both sides

$\underset{\delta x\rightarrow0}{lim}\frac{\phi(x+\delta x)-\phi(x)}{\delta x}=\underset{\delta x\rightarrow0}{lim}\left[\frac{\lbrack f(x+\delta x)-f(x)\rbrack}{\delta x}+\frac{\lbrack g(x+\delta x)-g(x)\rbrack}{\delta x}\right]$

$\underset{\delta x\rightarrow0}{lim}\frac{\phi(x+\delta x)-\phi(x)}{\delta x}=\underset{\delta x\rightarrow0}{lim}\left[\frac{\lbrack f(x+\delta x)-f(x)\rbrack}{\delta x}\right]+\underset{\delta x\rightarrow0}{lim}\left[\frac{\lbrack g(x+\delta x)-g(x)\rbrack}{\delta x}\right]$