derivative of inverse hyperbolic functions
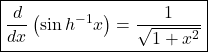 where
where ![]()
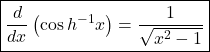 where
where ![]()

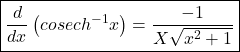 where
where ![]()
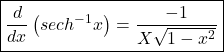 where
where ![]()
![]() where
where ![]()
![]() where
where ![]()
Derivatives of sin inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
![]()
Now by using formula.
![]()
Now by using eq(1)
![]()
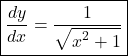
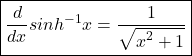
Derivatives of cos inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
![]()
Now by using formula.
![]()
Now by using eq(1)
![]()
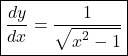
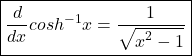
Derivatives of Tan inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
![]()
Now by using formula.
![]()
Now by using eq(1)
![]()
![]()
![]()
Derivatives of cosec inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
Now by using formula.
![]()
![]()
Now by using eq(1)
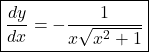
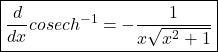
Derivatives of sec inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
Now by using formula.
![]()
![]()
Now by using eq(1)
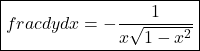
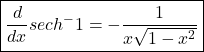
Derivatives of cot inverse hyperbolic function
Let.
![]()
![]()
Differentiating w.r.t x
![]()
![]()
![]()
![]()
Now by using formula.
![]()
Now by using eq(1)
![]()
![]()
![]()
These are the required derivative of inverse hyperbolic functions we should know.
