Now let us discuss the Conditional Statement.
A compound statement of the form if p then q, also written p implies q, is called a
conditional or an implication, p is called the antecedent or hypothesis and q is called the
consequent or the conclusion.
A conditional is regarded as false only when the antecedent is true and the consequent is false. In all other cases, it is considered to be true. Its truth table is, therefore, of the adjoining form. Entries in the first two rows are quite inconsonant with common sense but the entries of the last two rows seem to be against common sense. According to the third row the conditional If p then q is true when p is false and q is true and the compound proposition
is true (according to the fourth row of the table) even when both its components are false. We attempt to clear the position with the help of Table (4) of an example. Consider the conditional If a person A lives at Lahore, then he lives in Pakistan. If the antecedent is false i.e., A does not live in Lahore, all the same, he may be living in Pakistan. We have no reason to say that he does not live in Pakistan. We cannot, therefore, say that the conditional is false. So we must regard it as true. It must be remembered that we are discussing a problem of Aristotelian logic in which every proposition must be either true or false and there is no third possibility. In the case under discussion there being no reason to regard the proposition as false, it has to be regarded as true. Similarly, when both the antecedent and consequent of the conditional under consideration are false, there is no justification for quarreling with the proposition.
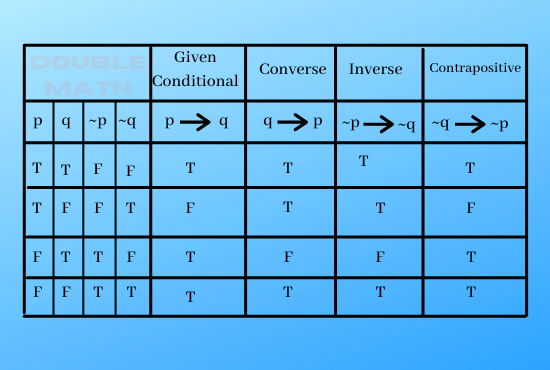
Conditionals related with a given conditional.
Let ![]() be a given conditional. Then
be a given conditional. Then
i) ![]() is called the converse of
is called the converse of ![]()
ii) ![]() is called the inverse of
is called the inverse of ![]()
iii) ![]() is called the contrapositive of
is called the contrapositive of ![]() .
.
To compare the truth values of these new conditionals with those of ![]() we draw up their joint table
we draw up their joint table
From the table, it appears that
i) Any conditional and its contrapositive are equivalent therefore any theorem may be
proved by proving its contrapositive.
ii) The converse and inverse are equivalent to each other.
Biconditional Statement:
Here we can discuss the most important geometry topics that are Biconditional Statement & Conditional Statement you must know. Let’s discuss the topic.
![]()
The proposition ![]() is shortly written
is shortly written ![]() and is called the biconditional statement.
and is called the biconditional statement.
or equivalence. It is read p if q (iff stands for “if and only if ’’)

We draw up its truth table as
