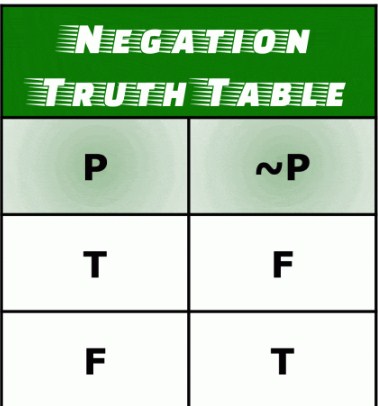
Negation:
If p is any proposition its negation is denoted by ~p, read
‘not p‘. It follows from this definition that if p is true, ~p is false and if
p is false, ~p is true. The adjoining table, called the truth table, gives the
possible truth- values of p and ~p.
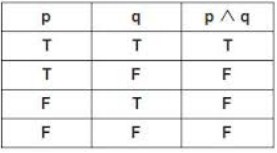
Conjunction:
The conjunction of two statements p and q is denoted symbolically as
p/q (p and q). Conjunction is considered to be true only if both
its components are true. So the truth table of p /
Disjunction:
Disjunction of p and q is p or q. It is symbolically written p ∨ q.
The disjunction p ∨ q is considered to be true when at least one
of the components p and q is true. It is false when both of them
are false.

You can also check Biconditional Statement
further, to check similar topic here
