What is Geometry in Math: Geometry is one of the most ancient branches of mathematics. The Greeks systematically studied it about four centuries B.C. Most of the geometry taught in schools is due to Euclid who expounded thirteen books on the subject (300 B.C.). A French philosopher and mathematician Rene Descartes (1596-1650 A.D.) introduced algebraic methods in
geometry which gave birth to analytical geometry (or coordinate geometry).
Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids, and higher dimensional analogs.
Our aim is to present the fundamentals of the subject in this blog.
Coordinate System (Geometry)
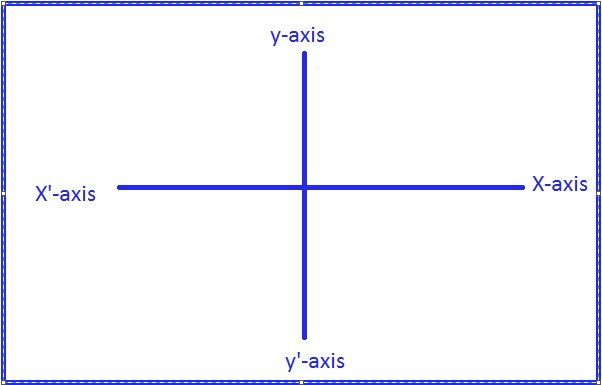
Draw in a plane two mutually perpendicular number lines ![]() and
and ![]() , one horizontal and the other vertical. Let their point of intersection be
, one horizontal and the other vertical. Let their point of intersection be ![]() , to which we call the origin and the real number 0 of both the lines is represented by O. The two lines are called the coordinate axes. The horizontal line
, to which we call the origin and the real number 0 of both the lines is represented by O. The two lines are called the coordinate axes. The horizontal line ![]() is called the x-axis and the vertical line
is called the x-axis and the vertical line ![]() is called the y-axis.
is called the y-axis.
As in the case of a number line, we follow the convention that all points on the y-axis above ![]() are associated with positive real numbers, those below
are associated with positive real numbers, those below ![]() with negative real numbers. Similarly, all points on the x-axis and lying on the right of O will be positive and those on the left of O and lying on the x-axis will be negative.
with negative real numbers. Similarly, all points on the x-axis and lying on the right of O will be positive and those on the left of O and lying on the x-axis will be negative.

Suppose P is any point in the plane. Then P can be located by using an ordered pair of real numbers. Through P draw lines parallel to the coordinates axes meeting x-axis at R and y-axis at S.
Let the directed distance ![]() and the directed distance
and the directed distance ![]() .
.
The ordered pair ![]() gives us enough information to locate the point P. Thus, with
gives us enough information to locate the point P. Thus, with
every point P in the plane, we can associate an ordered pair of real numbers (x, y) and we say that P has coordinates ![]() . It may be noted that
. It may be noted that ![]() and
and ![]() is the directed distances of P from the y-axis and the x-axis respectively. The reverse of this technique also provides a method for associating exactly one point in the plane with any ordered pair (x, y) of real numbers. This method of pairing off in a one-to-one function the points in a plane with ordered pairs of real numbers is called the two-dimensional rectangular (or Cartesian) coordinate system. If
is the directed distances of P from the y-axis and the x-axis respectively. The reverse of this technique also provides a method for associating exactly one point in the plane with any ordered pair (x, y) of real numbers. This method of pairing off in a one-to-one function the points in a plane with ordered pairs of real numbers is called the two-dimensional rectangular (or Cartesian) coordinate system. If ![]() are the coordinates of a point P, then the first member (component) of the ordered pair is called the x – coordinate or abscissa of P and the second member of the ordered pair is called the y – coordinate or ordinate of P. Note that abscissa is always first element and the ordinate is the second element in an ordered pair. The coordinate axes divide the plane into four equal parts called quadrants. They are denied as follows:
are the coordinates of a point P, then the first member (component) of the ordered pair is called the x – coordinate or abscissa of P and the second member of the ordered pair is called the y – coordinate or ordinate of P. Note that abscissa is always first element and the ordinate is the second element in an ordered pair. The coordinate axes divide the plane into four equal parts called quadrants. They are denied as follows:
Quadrant:
Quadrant I: All points ![]() with
with ![]()
Quadrant II: All points ![]() with
with ![]()
Quadrant III: All points ![]() with
with ![]()
Quadrant IV: All points ![]() with
with ![]()
The point P in the plane that corresponds to an ordered pair ![]() is called the graph of
is called the graph of ![]() . Thus given a set of ordered pairs of real numbers, the graph of the set is the aggregate of all points in the plane that correspond to ordered pairs of the set. also, check Wikipedia.
. Thus given a set of ordered pairs of real numbers, the graph of the set is the aggregate of all points in the plane that correspond to ordered pairs of the set. also, check Wikipedia.
for further detail, you can also check here.
