Binomial expansion:
\boxed{\left(1+x\right)^n=1+nx+\frac{n\left(n-1\right)}{2!}x^2+\frac{n\left(n-1\right)\left(n-2\right)}{3!}x^3+…….}
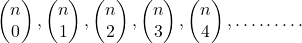\begin{pmatrix}n\\0\end{pmatrix},\begin{pmatrix}n\\1\end{pmatrix},\begin{pmatrix}n\\2\end{pmatrix},\begin{pmatrix}n\\3\end{pmatrix},\begin{pmatrix}n\\4\end{pmatrix},……… are called meaningless when 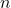n is negative or fraction
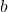a and b are exponents and 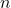n is called index.
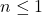n\leq1 index is always less then one.
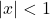\left|x\right|<1 exponent is always less then one.
This series is called Binomial series.
Example:
using Binomial expansion solve this:
\boxed{\left(1-x\right)^\frac12}
HERE
\boxed{1=1} \boxed{x=-x} \boxed{n=\frac12}using Binomial expansion formula
\boxed{\left(1+x\right)^n=1+nx+\frac{n\left(n-1\right)}{2!}x^2+\frac{n\left(n-1\right)\left(n-2\right)}{3!}x^3+…….}
\boxed{\left(1-x\right)^\frac12=1+\left(\frac12\right)\left(-x\right)+\frac{\left({\displaystyle\frac12}\right)\left({\displaystyle\frac12}-1\right)}{2!}\left(-x\right)^2+\frac{\left({\displaystyle\frac12}\right)\left({\displaystyle\frac12-1}\right)\left({\displaystyle\frac12}-2\right)}{3!}\left(-x\right)^3+….}
\boxed{\left(1-x\right)^\frac12=1+\left(\frac12\right)\left(-x\right)+\frac{\left({\displaystyle\frac12}\right)\left({\displaystyle\frac12}-1\right)}{2!}\left(x\right)^2-\frac{\left({\displaystyle\frac12}\right)\left({\displaystyle\frac12-1}\right)\left({\displaystyle\frac12}-2\right)}{3!}\left(x\right)^3+….} \boxed{\left(1-x\right)^\frac12=1+\left(\frac12\right)\left(-x\right)+\frac{\left({\displaystyle\frac12}\right)\left(-{\displaystyle\frac12}\right)}2x^2-\frac{\left({\displaystyle\frac12}\right)\left({\displaystyle-\frac12}\right)\left({\displaystyle\frac{-3}2}\right)}6x^3+….} \boxed{\left(1-x\right)^\frac12=1+\left(\frac12\right)\left(-x\right)+\frac{\displaystyle\frac14}2x^2-\frac{\displaystyle\frac38}6x^3+….} \boxed{\left(1-x\right)^\frac12=1+\left(\frac12\right)\left(-x\right)+\frac1{4.2}x^2-\frac3{8.6}x^3+…..} \boxed{\left(1-x\right)^\frac12=1-\frac12x+\frac18x^2-\frac1{16}x^3+….}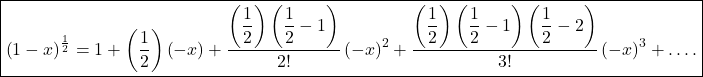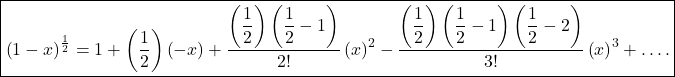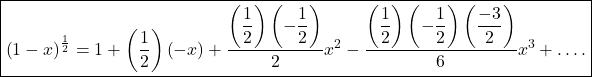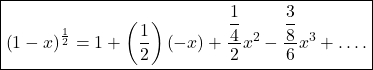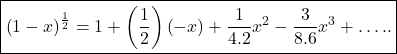This is required binomial series.