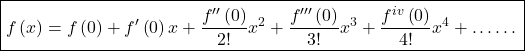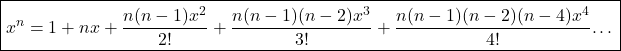Maclaurin series expension.
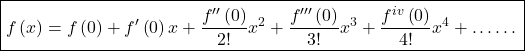
The expension of ![]() is called the Maclaurin series expension.
is called the Maclaurin series expension.
The above expansion is called Maclaurin Theorem.
Example
![]()
Apply Maclaurin series expension.
![]()
Add title
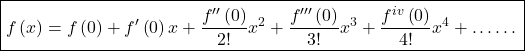
The expension of ![]() is called the Maclaurin series expension.
is called the Maclaurin series expension.
The above expansion is called Maclaurin Theorem.
Example
![]()
Apply Maclaurin series expension.
![]()
![]()
![]()
![]()
Put ![]() above equations
above equations
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Substituting these values in the formula.
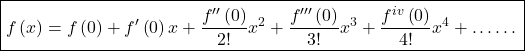
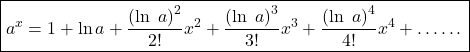
Example
![]()
![]()
Apply Maclaurin series expension.
![]()
![]()
![]()
![]()
Put ![]() above equations
above equations
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Substituting these values in the formula.