Derivative of Hyperbolic Functions with Examples

Here we will discuss the derivative of hyperbolic functions:

$\boxed{\frac d{dx}\left(\sin hx\right)=\cos hx}$

$\boxed{\frac d{dx}\left(\cos hx\right)=\sin hx}$

$\boxed{\frac d{dx}\left(\tan hx\right)=sec^2hx}$

$\boxed{\frac d{dx}\left(cothx\right)=-cosec^2hx}$

$\boxed{\frac d{dx}\left(sechx\right)=-sechx.\tan hx}$

$\boxed{\frac d{dx}\left(cosechx\right)=-cosechx.cothx}$

Derivative of sin hyperbolic functions:

$\frac d{dx}\left(\sin hx\right)=\cos hx$

$\sin hx=\left(\frac{e^x-e^{-x}}2\right)$

differentiating w.r.t x

$\frac d{dx}\sin hx=\frac d{dx}\left(\frac{e^x-e^{-x}}2\right)$

$\frac d{dx}\sin hx=\frac12\frac d{dx}\left(e^x-e^{-x}\right)$

Now by using the sum and difference rule.

$\frac d{dx}\sin hx=\frac12\left[\frac d{dx}e^x-\frac d{dx}e^{-x}\right]$

$\frac d{dx}\sin hx=\frac12\left[e^x-e^{-x}\left(-1\right)\right]$

$\frac d{dx}\sin hx=\frac12\left(e^x+e^{-x}\right)$

$\boxed{\frac d{dx}\sin hx=\frac{e^x+e^{-x}}2}$

$\boxed{\frac d{dx}\sin hx=\cos hx}$

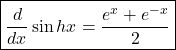
This is required derivative of sinhx.

Derivative of cos hyperbolic functions:

$\frac d{dx}\left(\cos hx\right)=\sin hx$

$\cos hx=\left(\frac{e^x+e^{-x}}2\right)$

differentiating w.r.t x

$\frac d{dx}\sin hx=\frac d{dx}\left(\frac{e^x+e^{-x}}2\right)$

$\frac d{dx}\sin hx=\frac12\frac d{dx}\left(e^x+e^{-x}\right)$

Now by using the sum and difference rule.

$\frac d{dx}\cos hx=\frac12\left[\frac d{dx}e^x+\frac d{dx}e^{-x}\right]$

$\frac d{dx}\cos hx=\frac12\left[e^x+e^{-x}\left(-1\right)\right]$

$\frac d{dx}\cos hx=\frac12\left(e^x-e^{-x}\right)$

$\boxed{\frac d{dx}\cos hx=\frac{e^x-e^{-x}}2}$

$\boxed{\frac d{dx}\cos hx=\sin hx}$

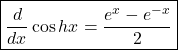
This is required derivative of coshx.

Derivative of Tanhx:

$\boxed{\frac d{dx}\left(\tan hx\right)=sec^2hx}$

$Tanhx=\frac{\sin hx}{\cos hx}$

$\frac{\sin hx}{\cos hx}=\frac{\displaystyle\frac{e^x-e^{-x}}2}{\displaystyle\frac{e^x+e^{-x}}2}$

$\frac{\sin hx}{\cos hx}==\frac{e^x-e^{-x}}2\times\frac2{e^x+e^{-x}}$

$Tanhx=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

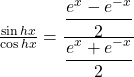
differentiating w.r.t x

$\frac d{dx}Tanhx=\frac d{dx}\left[\frac{e^x-e^{-x}}{e^x+e^{-x}}\right]$

Now by using the quotient rule.

$\frac d{dx}Tanhx=\frac{\left(e^x+e^{-x}\right).{\displaystyle\frac d{dx}}\left(e^x-e^{-x}\right)-\left(e^x-e^{-x}\right).{\displaystyle\frac d{dx}}\left(e^x+e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac{\left(e^x+e^{-x}\right).\left(e^x-e^{-x}\times-1\right)-\left(e^x-e^{-x}\right).\left(e^x+e^{-x}\times-1\right)}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac{\left(e^x+e^{-x}\right).\left(e^x+e^{-x}\right)-\left(e^x-e^{-x}\right).\left(e^x-e^{-x}\right)}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac{\left(e^x+e^{-x}\right)^2-\left(e^x-e^{-x}\right)^2}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac{\left(e^{2x}+e^{-2x}+2\right)-\left(e^{2x}-e^{-2x}-2\right)}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac{e^{2x}+e^{-2x}+2-e^{2x}-e^{-2x}+2}{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\frac4{\left(e^x+e^{-x}\right)^2}$

$\frac d{dx}Tanhx=\left(\frac2{e^x+e^{-x}}\right)^2$

$\boxed{\frac d{dx}Tanhx=sech^2x}$

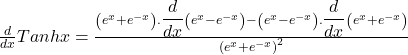
This is required derivative of Tanhx.

Derivative of cosec hyperbolic functions:

$\boxed{\frac d{dx}\left(cosechx\right)=-cosechx.cothx}$

As we know that

$\cos echx=\frac2{e^x-e^{-x}}$

$\frac d{dx}\cos echx=\frac d{dx}\left(\frac2{e^x-e^{-x}}\right)$

$\frac d{dx}\cos echx=2\frac d{dx}\left(\frac1{e^x-e^{-x}}\right)$

$\frac d{dx}\cos echx=2\frac d{dx}\left(e^x-e^{-x}\right)^{-1}$

Now by using power rule:

$\frac d{dx}\cos echx=2.(-1)\left(e^x-e^{-x}\right)^{-2}.\frac d{dx}(e^x-e^{-x})$

$\frac d{dx}\cos echx=2.(-1)\left(e^x-e^{-x}\right)^{-2}.(e^x-e^{-x}\times-1)$

$\frac d{dx}\cos echx=2.(-1)\left(e^x-e^{-x}\right)^{-2}.(e^x+e^{-x})$

$\frac d{dx}\cos echx=-2.\frac{(e^x+e^{-x})}{\left(e^x-e^{-x}\right)^2}$

$\frac d{dx}\cos echx=-\frac2{\left(e^x-e^{-x}\right)}.\frac{(e^x+e^{-x})}{\left(e^x-e^{-x}\right)}$

$\boxed{\frac d{dx}\cos echx=-\cos echx.cothx}$

This is required derivative of cosechx.

Derivative of sec hyperbolic functions:

$\boxed{\frac d{dx}\left(sechx\right)=-sechx.tanhx}$

As we know that:

$sechx=\frac2{e^x+e^{-x}}$

$\frac d{dx}sechx=\frac d{dx}\left(\frac2{e^x+e^{-x}}\right)$

$\frac d{dx}sechx=2\frac d{dx}\left(\frac1{e^x+e^{-x}}\right)$

$\frac d{dx}sechx=2\frac d{dx}\left(e^x+e^{-x}\right)^{-1}$

Now by using power rule:

$\frac d{dx}sechx=2.(-1)\left(e^x+e^{-x}\right)^{-2}.\frac d{dx}(e^x+e^{-x})$

$\frac d{dx}sechx=2.(-1)\left(e^x+e^{-x}\right)^{-2}.(e^x+e^{-x}\times-1)$

$\frac d{dx}secchx=2.(-1)\left(e^x+e^{-x}\right)^{-2}.(e^x-e^{-x})$

$\frac d{dx}sechx=-2.\frac{(e^x+e^{-x})}{\left(e^x-e^{-x}\right)^2}$

$\frac d{dx}sechx=-\frac2{\left(e^x+e^{-x}\right)}.\frac{(e^x+e^{-x})}{\left(e^x-e^{-x}\right)}$

$\boxed{\frac d{dx}\cos echx=-\cos echx.cothx}$

This is required derivative of sechx.

Derivative of cot hyperbolic functions:

$\boxed{\frac d{dx}\left(\cot hx\right)=cosec^2hx}$

$cothx=\frac{\cos hx}{\sin hx}$

$\frac{\cos hx}{\sin hx}=\frac{\displaystyle\frac{e^x+e^{-x}}2}{\displaystyle\frac{e^x-e^{-x}}2}$

$\frac{\cos hx}{\sin hx}==\frac{e^x+e^{-x}}2\times\frac2{e^x-e^{-x}}$

$cothx=\frac{e^x+e^{-x}}{e^x-e^{-x}}$

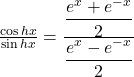
differentiating w.r.t x

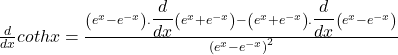
$\frac d{dx}cothx=\frac d{dx}\left[\frac{e^x+e^{-x}}{e^x-e^{-x}}\right]$

Now by using quotient rule.

$\frac d{dx}cothx=\frac{\left(e^x-e^{-x}\right).{\displaystyle\frac d{dx}}\left(e^x+e^{-x}\right)-\left(e^x+e^{-x}\right).{\displaystyle\frac d{dx}}\left(e^x-e^{-x}\right)}{\left(e^x-e^{-x}\right)^2}$

$\frac d{dx}cothx=\frac{\left(e^x-e^{-x}\right).\left(e^x+e^{-x}\times-1\right)-\left(e^x+e^{-x}\right).\left(e^x-e^{-x}\times-1\right)}{\left(e^x-e^{-x}\right)^2}$