Introduction
Let ![]() be a complex variable of
be a complex variable of ![]() .The function Imaginary Error Function
.The function Imaginary Error Function
erfi is defined by the following second-order differential equation
![]() ———-(1)
———-(1)

The initial condition of (1) at 0 is
![]()
![]()
Series and Asymptotic Expansions
2.1 Taylor expansion at 0.
2.1.1 First terms.
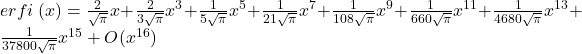
2.1.2 General form.
![]()
The coefficients u(n) satisfy the recurrence
![]() —————(.2.1.2.2)
—————(.2.1.2.2)
Initial conditions of 2.1.2.2 are given by
![]()
![]()
Erf Imaginary Error Function for Floating-Point and Symbolic Numbers:
Depending on its logic, erf can return floating-point or exact symbolic results. Work out the imaginary error function for these numbers. Because these numbers are not symbolic objects, you get floating-point results.
![]()
![]()
Evaluate the imaginary error function for the same numbers converted to symbolic objects. For most symbolic numbers, erf x returns undetermined symbolic calls.
Imaginary Error Function for Variables and Expressions:
Compute the imaginary error function for x and ![]() . For most symbolic variables and expressions, erfi x returns unresolved symbolic calls.
. For most symbolic variables and expressions, erfi x returns unresolved symbolic calls.
syms
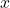
;
.
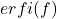
ans =
erfi(x) .
ans =
erfi(sin(x) + x*e^x
“Error Function”
In mathematics, the error function is also called the Gauss error function. often denoted by erf, is a complex function of a complex variable defined as
![]() .
.
This integral is a special function that occurs often in calculus. In calculus, a function argument is a real number. If the function argument is real, then the function value is also a real number.
Properties:
The property ![]() means that the error function is an odd function. This directly results from the fact that the integrand
means that the error function is an odd function. This directly results from the fact that the integrand ![]() is an even (integrating an even function gives an odd function and vice versa.
is an even (integrating an even function gives an odd function and vice versa.
For complex number ![]() :
:
![]() .
.
where ![]() is complex conjugate of
is complex conjugate of ![]()
for math, basic knowledge click here
