Translation of Axes: Let xy-coordinate system be given and O'( h,k) be any point in the plane. Through O' draw two mutually perpendicular lines O'X, O'Y such that O'X is parallel to Ox . The new axes O'X and O'Y are called translation of the Ox and Oy axes through the point O' . In this, the origin is shifted to another point in the plane but the axis remains parallel to the old axes. Let P be a point with coordinates (x,y ) referred to xy -coordinate system and the axes be translated through the point O'(h ,k ) and O'X, O'Y be the new axes. If P has coordinates (X, Y) referred to the new axes, then we need to find X, Y in terms of x, y.
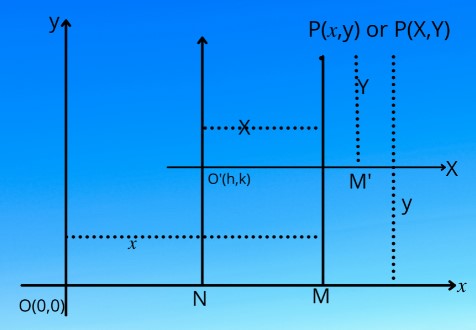
Translation of Axes
Draw PM and O' N perpendiculars to Ox .
From the figure, we have
OM =x,\;\;\;\;\;MP= y,\;\;\;\;\;ON= h,\;\;\;\;\;NO'= k =MM' .
Now
X =O'M' =NM= OM -OM- ON =x -h.
Similarly,
Y =M' P =MP- MM'= y -k
Thus the coordinates of P referred to XY-system are (x-h,y-k ).
i.e,X= x-h
Y= y-k .
Moreover,
\boxed{x= X+ h \;\;\;\;and\;\;\;\; y=Y+k}
Example 1:(Translation of Axes)
The coordinates of a point P are (-6, 9). The axes are translated through the point O' (-3, 2). Find the coordinates of Preferred to the new axes.
Solution:
Here
h=-3\;\;\; and\;\;\;\; k= 2
Coordinates of P referred to the new axes are (X, Y) given by
X =x-h= -6 - (-3) = -3
And
Y =y-k= 9 - 2 = 7
Thus
\boxed{P (X, Y) = P (-3 ,7)}.
Example 2: (Translation of Axes)
The xy -coordinate axes are translated through the point O' (4, 6). The coordinates of the point P are (2, -3) referred to as the new axes. Find the coordinates of Preferred to the original axes.
Solution:
Here
X=2, \;\;,Y=-3\;,\;h=4 ,\;\;k =6 .
We have
x=X+h = 4+2= 6
y=Y+k = -3+6=3
Thus required coordinates are \boxed{P (6, 3)}
Wikipedia. Do you want to read the geometry topic click here