Field definition math: A set S is called a field if the operations of addition ‘+ ’ and multiplication ‘. ’ on S satisfy
the following properties are written in tabular form:
| Addition |
| Closure for any set S\: a,b\in S \newline a+b \in S Commutativity for any \: a,b\in S \newline a+b = b+a Associativity for any \: a,b,c\in S \newline \left ( a+b \right )+c = a+\left ( b+c \right ) Existence of Identity for any a\in S\: \exists \: 0\in S such that a+0=0+a=a Existence of Inverses for any a\in S\:\: \: \exists \: -a\in S such that a+\left ( -a \right )=\left ( -a \right )a=0 Distributivity for any 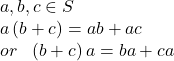a,b,c\in S \newline a\left ( b+c \right )=ab+ac \newline or\: \: \: \left ( b+c \right )a=ba+ca |
| Multiplication |
| closure for any set S\: a,b\in S \newline a\times b \in S Commutativity for any \: a,b\in S \newline a\times b = b\times a Associativity for any \: a,b,c\in S \newline \left ( a+b \right )+c = a+\left ( b+c \right ) Existence of Identity for any a\in S\: \exists \: 1\in S such that a.1=1.a=a Existence of Inverses for any a\in S\:\: \:;a\neq 0\: \: \exists \:\: \: \frac{1}{a}\in S such that a\left ( \frac{1}{a} \right )= \left ( \frac{1}{a} \right )a= 1 Distributivity for any 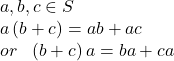a,b,c\in S \newline a\left ( b+c \right )=ab+ac \newline or\: \: \: \left ( b+c \right )a=ba+ca |
All the above mentioned properties hold for \Re \: \: \:\: \mathbb{C}\: \: \: \: \mathbb{Q}.
Hence \Re \: \: \:\: \mathbb{C}\: \: \: \: \mathbb{Q} are a field in math