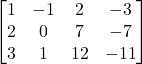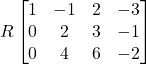Rank of a Matrix: Let M be a non-zero matrix. If r is the number of non-zero rows when it is
reduced to the reduced echelon form, then r is called the (row) rank of the matrix M.
Example:
Find rank the rank of matrix 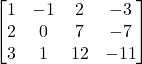
Solution:
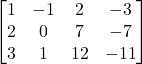
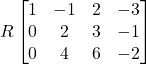
Rank of a Matrix: Let M be a non-zero matrix. If r is the number of non-zero rows when it is
reduced to the reduced echelon form, then r is called the (row) rank of the matrix M.
Example:
Find rank the rank of matrix 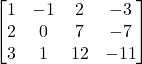
Solution: