How to Solve SSS Triangle

Leave a Comment / Mathematics / By Azhar

“SSS” means side, side, side.

“SSS” is used when three sides of a triangle are given and we want to find the missing angles. Consider the triangle $\triangle ABC$ with the side $a$ , $b$ and $c$ and angle $\alpha$ , $\beta$ and $\gamma$ .We can observe that we are given the three sides $a$ , $b$ and $c$ . Therefore the figure illustrates a triangle combination which is known as a SSS triangle.

How to Solve SSS Triangle

To solve an SSS triangle:

Step 1: First we use the “Law of cosine ” to find an angle.

Step 2: Secondly use again “Law of cosine ” to find another angle.

Step 3: Finally use angles of triangles added to 180 to find the last angle.

We use the “angle” version of the Law of Cosines:

$\cos\alpha=\frac{b^2+c^2-a^2}{2bc}$ .
$\cos\beta=\frac{a^2+c^2-b^2}{2ac}$ .
$\cos\gamma=\frac{a^2+b^2-c^2}{2ab}$ .

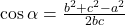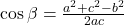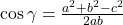Example No.1

(By using Law of cosine)

when three sides are given.

a=7 , b=3 , c=5

$\cos\alpha=\frac{b^2+c^2-a^2}{2bc}$ .

By putting the values

$\cos\alpha=\frac{3^2+5^2-7^2}{2(3)(5)}$ .

$\Rightarrow\cos\alpha=\frac{9+25-49}{30}$ .

$\Rightarrow\cos\alpha=\frac{-15}{30}$ .

$\Rightarrow\cos\alpha=\frac{-1}{2}$ .

$\Rightarrow\alpha\;\;\;=\cos^{-1}(\frac{-1}2)$ .

$\Rightarrow\boxed{\alpha\;=120^o}$ .

Now,

$\cos\beta=\frac{c^2+a^2-b^2}{2ca}$ .

using values

$\cos\beta=\frac{5^2+7^2-3^2}{2(5)(7)}$ .

$\Rightarrow\cos\beta=\frac{25+49-9}{70}$ .

$\Rightarrow\cos\beta=\frac{65}{70}$ .

$\Rightarrow\cos\beta=0.9286$ .

$\Rightarrow\beta\;\;\;=\cos^{-1}(0.9286)$ .

$\Rightarrow\boxed{\beta\;=1^o}$ .

Now, we know that

$\alpha +\beta+ \gamma=180^o$ .

$\gamma=180^o-\alpha -\beta$ .

$\gamma=180^o-120^o -1^o$ .

$\Rightarrow\boxed{\gamma=59^o}$ .

Leave a Comment Cancel Reply