Semi Group, Definition and Examples:-

Definition: A non empty set G having binary operation “*” (say) is called semi group in math if it satisfies the following two axioms:

• Closure Property w.r.t “*“

i.e, a\ast b\in G\;\;\;\;\;\;\;\forall\;a,b\in G

• Associative Law w.r.t “*“

(a\ast b)\ast c=a\ast(b\ast c)\;\;\;\;\;\;:\;\forall\;a,b,c\in G

Examples of Semi Group:

• The set of W- {0,1} with respect to “Addition” and “Multiplication”.
• The set of Natural Number with respect to “Addition”.
• The set of 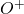O^+ with respect to “Addition”.