How to Find the Area of Kite?

Kite

A Kite is a flat shape with straight sides. It has two pairs of equal length with adjacent sides. 

Properties of a kite

• A kite has two pairs of sides.
• Two pairs are equal in length and both sides are adjacent.
• Where two pairs of sides meet the angles are equal.
• Diagonals cross at right angles.

Area of a Kite

Space enclosed by a kite is called its area. A kite has 4 angles, 4 sides, and 2 diagonals. The area of the square is always expressed in square units like

Area of a kite = \frac12\;D_1D_2

How to derive a formula to find the area of a kite

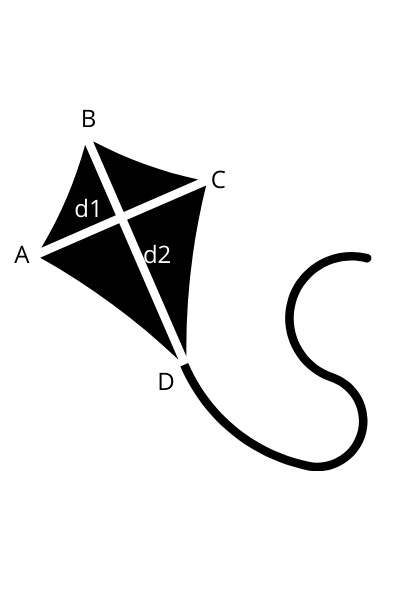
We want to find the area of a kite ABCD  

The length of the diagonals of ABCD to be AC=p and BD = q

Longer diagonal bisects the shorter diagonal at a right angle that is BD bisect AC and ∠AOB=90° ,    ∠BOC=90° 

So,

AO=OC=AC/2 =p/2

Area of kite = Area of triangle ABD + Area of triangle BCD…….(1)

Area of triangle = ½  (base)(height)

Area of triangle ABD = ½ (AO)(BD)

                                     = ½ (p/2) (q)

                                      = (pq)/4

Area of triangle BCD = ½ (OC)(BD)

                                     = ½ (p/2) (q)

                                      = (pq)/4

By using eq. 1

Area of kite ABCD= (pq)/4+(pq)/4

                                = (pq)/2

As we know 

p=AC     ,q = BD

Area of kite = ½ (AC)(BD)